
 经过点B、E,若C′、D′在y轴上,则k= .
经过点B、E,若C′、D′在y轴上,则k= .
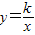 经过点B、E,
经过点B、E,
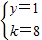


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案科目:初中数学 来源: 题型:
 度不考虑)
度不考虑)查看答案和解析>>
科目:初中数学 来源: 题型:
 如图矩形ABCD中长AB=6、宽AD=2,将矩形ABCD绕A逆时针旋转90°到矩形AB′C′D′,E是AB′的中点,若双曲线y=
如图矩形ABCD中长AB=6、宽AD=2,将矩形ABCD绕A逆时针旋转90°到矩形AB′C′D′,E是AB′的中点,若双曲线y=| k | x |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
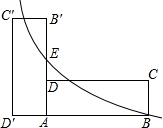 如图矩形ABCD中长AB=6、宽AD=2,将矩形ABCD绕A逆时针旋转90°到矩形AB′C′D′,E是AB′的中点,若双曲线
如图矩形ABCD中长AB=6、宽AD=2,将矩形ABCD绕A逆时针旋转90°到矩形AB′C′D′,E是AB′的中点,若双曲线 经过点B、E,若C′、D′在y轴上,则k=________.
经过点B、E,若C′、D′在y轴上,则k=________.查看答案和解析>>
科目:初中数学 来源: 题型:
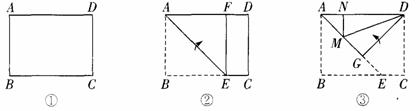
小明尝试着将矩形纸片ABCD(如图①,AD>CD)沿过点A的直线折叠,使点B落在AD边上的点F处,折痕为AE(如图②);再沿过点D的直线折叠,使得点C落在DA边上的点N处,点E落在AE边上的点M处,折痕为DG(如图③).如果第二次折叠后,点M正好在![]() NDG的平分线上,那么矩形ABCD中长与宽的比值为_________.
NDG的平分线上,那么矩形ABCD中长与宽的比值为_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com