
科目:初中数学 来源: 题型:填空题
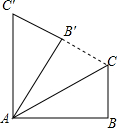 如图,在△ABC中,∠B=90°,将△ABC绕点A旋转至△AB′C′的位置,若AC′∥BC,C′B′的延长线过点C,则∠BAC的度数为30°.
如图,在△ABC中,∠B=90°,将△ABC绕点A旋转至△AB′C′的位置,若AC′∥BC,C′B′的延长线过点C,则∠BAC的度数为30°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在如图的正方形网格中,每个小正方形的边长均为1个单位,将△ABC绕点C逆时针旋转90°,得到△A′B′C′;再将△A′B′C′,向右平移2个单位,得到△A″B″C″;请你画出△A′B′C′和△A″B″C″(不要求写画法)
在如图的正方形网格中,每个小正方形的边长均为1个单位,将△ABC绕点C逆时针旋转90°,得到△A′B′C′;再将△A′B′C′,向右平移2个单位,得到△A″B″C″;请你画出△A′B′C′和△A″B″C″(不要求写画法)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
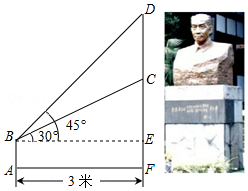 如图,某学校在“国学经典”中新建了一座吴玉章雕塑,小林站在距离雕塑3米的A处自B点看雕塑头顶D的仰角为45°,看雕塑底部C的仰角为30°,求塑像CD的高度.(最后结果精确到0.1米,参考数据:$\sqrt{3}$≈1.7)
如图,某学校在“国学经典”中新建了一座吴玉章雕塑,小林站在距离雕塑3米的A处自B点看雕塑头顶D的仰角为45°,看雕塑底部C的仰角为30°,求塑像CD的高度.(最后结果精确到0.1米,参考数据:$\sqrt{3}$≈1.7)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,曲线l是由函数y=$\frac{6}{x}$在第一象限内的图象绕坐标原点O逆时针旋转45°得到的,过点A(-4$\sqrt{2}$,4$\sqrt{2}}$),B(2$\sqrt{2}$,2$\sqrt{2}}$)的直线与曲线l相交于点M、N,则△OMN的面积为8.
如图,曲线l是由函数y=$\frac{6}{x}$在第一象限内的图象绕坐标原点O逆时针旋转45°得到的,过点A(-4$\sqrt{2}$,4$\sqrt{2}}$),B(2$\sqrt{2}$,2$\sqrt{2}}$)的直线与曲线l相交于点M、N,则△OMN的面积为8.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com