
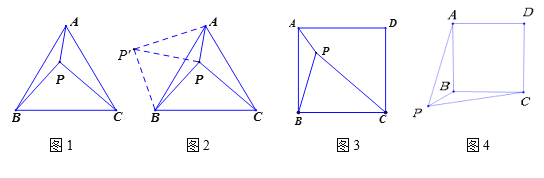
����Ŀ�����������������ѧ�������������ϣ�ij����С�����������һ�����⣺��ͼ1���ڵȱ�������ABC����һ��P����PA��1��PB��2��PC��![]() �����������APB�Ķ�����
�����������APB�Ķ�����
������������1������ͬѧ������Ŀ������PA��PB��PC�ij�Ϊ�ߵ���������ֱ�������Σ����ҵ�����ȷ��˼·����ͼ2������BPC�Ƶ�B��ʱ����ת60�����õ���BP��A������PP��������P��PB�ǵȱ������Σ���P��PA��ֱ�������Σ������BPP����_________����APB��_________��
��������ȣ���2��ͬ�������ͬѧͻȻ���������������һ�����⣺��ͼ3����P��������ABCD��һ�㣬PA=1��PB=2��PC=3������APB�Ķ���������д�������̣�
���������죩��3������ʦ����һ��˼���⣺��ͼ4������P��������ABCD��һ�㣬PA=![]() ��PB=1��PC=
��PB=1��PC=![]() ������APB�Ķ���������д�������̣�
������APB�Ķ���������д�������̣�
���𰸡���1��60����150������2����APB��135��������������3����APB��45����������
��������
��1������BPC�Ƶ�B��ʱ����ת60�����õ���BP��A������PP��������![]() ��
��![]() ��
��![]() ��
��![]() ���ɵ�
���ɵ�![]() �ǵȱ������Σ�����
�ǵȱ������Σ�����![]() ��
��![]() ����֤
����֤![]() ��ֱ�������Σ�����
��ֱ�������Σ�����![]() �ɵô𰸣�
�ɵô𰸣�
��2����![]() �Ƶ�
�Ƶ�![]() ��ʱ����ת
��ʱ����ת![]() ���õ���
���õ���![]() ������
������![]() ����
����![]() ��
��![]() ��
��![]() ��
��![]() ���ɵ�
���ɵ�![]() �����ݹ��ɶ����ã�
�����ݹ��ɶ����ã�![]() ������֤��
������֤��![]() ����
����![]() ��ֱ�������Σ���
��ֱ�������Σ���![]() ��
��
����![]() �ɵô𰸣�
�ɵô𰸣�
��3����![]() �Ƶ�
�Ƶ�![]() ��ʱ����ת
��ʱ����ת![]() ���õ���
���õ���![]() ������
������![]() ����
����![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() �����ݹ��ɶ����ã�
�����ݹ��ɶ����ã�![]() ����֤��
����֤��![]() ����
����![]() ��ֱ�������Σ���
��ֱ�������Σ���![]() ��
��
����![]() �ɵô𰸣�
�ɵô𰸣�
�⣺��1������BPC�Ƶ�B��ʱ����ת60�����õ���BP��A������PP����
����![]() ��
��![]() ��
��![]() ��
��![]() ��
��
��![]() �ǵȱ������Σ�
�ǵȱ������Σ�
��![]() ��
��![]() ��
��
��![]()
��![]() ��ֱ�������Σ�
��ֱ�������Σ�
��![]() ��
��
��![]() ��
��
��2����ͼʾ����![]() �Ƶ�
�Ƶ�![]() ��ʱ����ת
��ʱ����ת![]() ���õ���
���õ���![]() ������
������![]() ��
��
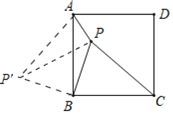
��![]() ��
��![]() ��
��![]() ��
��![]()
![]() ��
��
���ݹ��ɶ����ã�![]() ��
��
![]() ��
��
![]() ��
��
��![]() ��
��
![]() ��
��
![]() ��ֱ�������Σ���
��ֱ�������Σ���![]() ��
��
![]() ��
��
��3����ͼʾ����![]() �Ƶ�
�Ƶ�![]() ��ʱ����ת
��ʱ����ת![]() ���õ���
���õ���![]() ������
������![]() ��
��
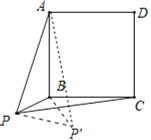
��![]() ��
��![]() ��
��![]() ��
��![]()
![]() ��
��
���ݹ��ɶ����ã�![]() ��
��
![]() ��
��
![]() ��
��
��![]()
![]() ��
��
![]() ��
��
![]() ��ֱ�������Σ���
��ֱ�������Σ���![]() ��
��
![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ABC��ֱ������ƽ���ڣ��������������ֱ�ΪA��0��3����B��3��4����C��2��2����������������ÿ��С�����εı߳���һ����λ���ȣ���
��1���Ե�BΪλ�����ģ��������ڻ�����A1B1C1��ʹ��A1B1C1���ABCλ�ƣ���λ�Ʊ�Ϊ2��1��
��2����C1���������� ������ ������
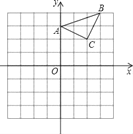
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������з��̣�
(1)x2��4x��5��0��(2)x(x��4)��2��8x��(3)x��3��4(x��3)2.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
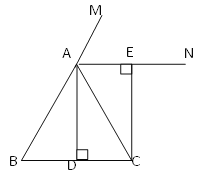
����Ŀ����ͼ��ʾ������ABC�У�ADƽ�֡�BAC��AD��BC������ΪD��AN����ABC��ǡ�CAM��ƽ���ߣ�CE��AN������ΪE.
��1����֤���ı���ADCE�Ǿ��Σ�
��2������ABC����ʲô����ʱ���ı���ADCE�������Σ�����֤��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾��֯����ְ������ǰ��ij���������ιۣ��μ���Ա��70�ˣ����ξ���涨������Ʊÿ��60Ԫ�����Żݣ�����ɽ��������������㰲�ŵĹ۹�������۹��С�ͳ������ͳ����࣬�ֱ�ɹ�4����11���˿ͳ�������С�ͳ�ÿ���շ�60Ԫ�����ͳ�ÿ���շ�10Ԫ����70����������ÿ�����Ҳι��������ܷ��ò�����5000Ԫ���ʾ��㰲�ŵ�С�ͳ������ͳ�����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С��Ҵ����ˢ���䣬������5�����ˣ�����10���깤������ij��Ϳ��150��������Ϊ4800Ԫ����ˢ�����Ϊ150![]() �������㹤Ǯʱ�����¼��ַ�����
�������㹤Ǯʱ�����¼��ַ�����
����1�������㣬ÿ����30Ԫ����1��������һ����һ������
����2����Ϳ�Ϸ����㣬Ϳ�Ϸ��õ�30%��Ϊ��Ǯ��
����3������ˢ����㣬ÿƽ������Ǯ12Ԫ��
�����С��ҳ����⣬ѡ�����ַ�����Ǯ����㣿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
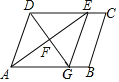
����Ŀ����ͼ���ı���ABCD��ƽ���ı��Σ�AEƽ�֡�BAD��CD�ڵ�E��AE�Ĵ�ֱƽ���߽�AB�ڵ�G����AE�ڵ�F����AD��4cm��BG��1cm����AB��_____cm��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У�ֱ��y����x+2��x�ᡢy��ֱ���A��B���㣬ֱ��BC��x�Ḻ�����ڵ�C����BCA��30������ͼ�٣�
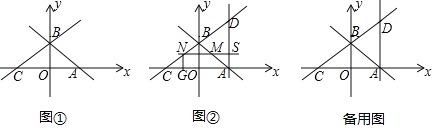
��1����ֱ��BC�Ľ���ʽ��
��2����ͼ���У�����A��x��Ĵ��߽�ֱ��CB�ڵ�D��������M�ӵ�A������������AB������ÿ��![]() ����λ���ȵ��ٶ��˶���ͬʱ������N�ӵ�C������������CB������ÿ��2����λ���ȵ��ٶ��˶���ֱ��MN��ֱ��AD���ڵ�S����ͼ�ڣ����˶�ʱ��Ϊt�룬����DSN�ա�BOCʱ����t��ֵ��
����λ���ȵ��ٶ��˶���ͬʱ������N�ӵ�C������������CB������ÿ��2����λ���ȵ��ٶ��˶���ֱ��MN��ֱ��AD���ڵ�S����ͼ�ڣ����˶�ʱ��Ϊt�룬����DSN�ա�BOCʱ����t��ֵ��
��3������M��ֱ��AB�ڵڶ������ϵ�һ�㣬��N��P�ֱ���ֱ��BC��ֱ��AD�ϣ��Ƿ������M��B��N��PΪ������ı��������Σ������ڣ���ֱ��д����M�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ϵ�![]() ��Ӧ�����ֱ���
��Ӧ�����ֱ���![]() ��
��![]() ��
��![]() Ϊ�������������㣬����ͬʱ�����˶�.��
Ϊ�������������㣬����ͬʱ�����˶�.��![]() �ӵ�
�ӵ�![]() �������ٶ�Ϊÿ��
�������ٶ�Ϊÿ��![]() ����λ���ȣ���
����λ���ȣ���![]() �ӵ�
�ӵ�![]() �������ٶ�Ϊ��
�������ٶ�Ϊ��![]() ��
��![]() ������
������![]() Ϊԭ��.
Ϊԭ��.
��1�����˶�![]() ��ʱ����
��ʱ����![]() ��Ӧ�����ֱ��� �� .
��Ӧ�����ֱ��� �� .
��2�����˶�������ʱ����![]() ��ǡ��һ����Ϊ���������������߶ε��е㣿
��ǡ��һ����Ϊ���������������߶ε��е㣿
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com