
【题目】已知一个二次函数图象上部分点的横坐标![]() 与纵坐标
与纵坐标![]() 的对应值如表所示:
的对应值如表所示:
| … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | … |
| … | 0 | ﹣3 | ﹣4 | ﹣3 | 0 | … |
(1)求这个二次函数的表达式;
(2)在给定的平面直角坐标系中画出这个二次函数的图象;
(3)当![]() 时,直接写出
时,直接写出![]() 的取值范围.
的取值范围.
科目:初中数学 来源: 题型:
【题目】如图,已知□ABCD的面积为100,P为边CD上的任一点,E,F分别为线段AP,BP的中点,则图中阴影部分的总面积为( )

A. 30B. 25C. 22.5D. 20
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题8分)如图,已知抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0)和点B(3,0),与y轴交于点C,连接BC交抛物线的对称轴于点E,D是抛物线的顶点.
(1)求此抛物线的解析式;
(2)直接写出点C和点D的坐标;
(3)若点P在第一象限内的抛物线上,且S△ABP=4S△COE,求P点坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】分类是研究问题的一种常用方法,我们在学习有理数和代数式的相关概念、运算法则时,除了 学到了具体知识,还学会了分类思考,在进行分类时,我们首先应明确分类标准,其次要做到分类时既不 重复,也不遗漏。
(初步感受)(1)在对多项式![]() ,
,![]() 进行分类时,如果以项数作为分类标准,可以分为哪几类?如果以次数作为分类标准,可以分为哪几类?
进行分类时,如果以项数作为分类标准,可以分为哪几类?如果以次数作为分类标准,可以分为哪几类?
(简单运用)(2)已知 a, b 是有理数,比较 a b 与 a b的大小;
(深入思考)(3)已知 a, b c 是有理数,且 ca b>ca b ,判断 b, c 的符号,并说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c (a、b、c为常数且a≠0)中的x与y的部分对应值如下表,
x | … | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | … |
y | … | 12 | 5 | 0 | -3 | -4 | -3 | 0 | 5 | 12 | … |
下列四个结论:
(1)二次函数y=ax2+bx+c 有最小值,最小值为-3;
(2)抛物线与y轴交点为(0,-3);
(3)二次函数y=ax2+bx+c 的图像对称轴是x=1;
(4)本题条件下,一元二次方程ax2+bx+c的解是x1=-1,x2=3.
其中正确结论的个数是( )
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 阅读材料:
为落实水资源管理制度,大力促进水资源节约,本市居民用水实行阶梯水价,按年度用水量计算,将居民家庭全年用水量划分为三档,水价分档递增,实施细则如表:

如某户居民去年用水量为190立方米,则其应缴纳水费为180×5+(190﹣180)×7=970元.
(1)若小明家去年用水量为100立方米,则小明家应缴纳的水费为________元;
(2)若截止10月底,小明家今年共纳水费1145元,则小明家共用水_______立方米;
(3)若小明家全年用水量x不超过270立方米,则应缴纳的水费为多少元?(用含x的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】央视热播节目“朗读者”激发了学生的阅读兴趣.某校为满足学生的阅读需求,欲购进一批学生喜欢的图书,学校组织学生会成员随机抽取部分学生进行问卷调查,被调查学生须从“文史类、社科类、小说类、生活类”中选择自己喜欢的一类,根据调查结果绘制了统计图(未完成),请根据图中信息,解答下列问题:
(1)此次共调查了 名学生;
(2)将条形统计图补充完整;
(3)图2中“小说类”所在扇形的圆心角为 度;
(4)若该校共有学生2500人,估计该校喜欢“社科类”书籍的学生人数.

查看答案和解析>>
科目:初中数学 来源: 题型:
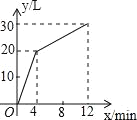
【题目】一个有进水管与出水管的容器,从某时刻开始4min内只进水不出水,在随后的8min内既进水又出水,每分钟进水量和出水量是两个常数.容器内的水量y(单位:L)与时间x(单位:min)之间的关系如图所示.
(1)求y关于x的函数解析式;
(2)每分钟进水、出水各多少升?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com