
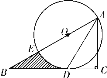
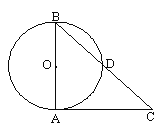
【题目】如图,已知点E在△ABC的边AB上,∠C=90°,以AE为直径的⊙O切BC于点D.
(1)求证:AD平分∠BAC;
(2)已知∠B=30°,AD=2![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
【答案】(1)证明见解析;(2) S阴影=2![]() -
-![]() .
.
【解析】
(1)连接OD,可证明OD∥AC,结合平行线的性质可证得结论;
(2)由直角三角形的性质可求得BD,再结合三角函数可求得OD,可求得△OBD和扇形OED的面积,可求得阴影部分面积.
(1)证明:如答图,连接OD.

∵BC为⊙O的切线,∴OD⊥BC.
又∵∠C=90°,∴OD∥AC,
∴∠ODA=∠DAC.
又∵OD=OA,∴∠OAD=∠ODA,
∴∠OAD=∠DAC,即AD平分∠BAC.
(2)解:∵∠B=30°,∴∠BAC=60°,
∴∠BAD=∠DAC=30°,∴BD=AD=2![]() .
.
在Rt△OBD中,tan B=,![]() 即
即![]() =
=![]() ,
,
∴OD=2,且∠BOD=60°,
∴S阴影=S△OBD-S扇形OED
=![]() ×2
×2![]() ×2-
×2-![]()
=2![]() -
-![]() .
.


科目:初中数学 来源: 题型:
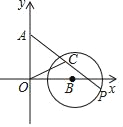
【题目】如图,在平面直角坐标系中,A(0,3)、B(3,0),以点B为圆心、2为半径的⊙B上有一动点P.连接AP,若点C为AP的中点,连接OC,则OC的最小值为( )
A. 1 B. ![]() ﹣1 C.
﹣1 C. ![]() D. 2
D. 2![]() ﹣1
﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
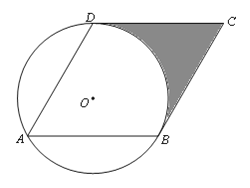
【题目】已知:如图,已知⊙O的半径为1,菱形ABCD的三个顶点A、B、D在⊙O上,且CD与⊙O相切.
(1)求证:BC与⊙O相切;
(2)求阴影部分面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1)是一个晾衣架的实物图,支架的基本图形是菱形,MN 是晾衣架的一个滑槽,点 P 在滑槽 MN 上、下移动时,晾衣架可以伸缩,其示意图如图(2)所示,已知每个菱形的边长均为 20cm,且 AB=CD=CP=DM=20cm.

(1)当点 P 向下滑至点 N 处时,测得 DCE 60 时.
①求滑槽 MN 的长度;
②此时点 A 到直线 DP 的距离是多少?
(2)当点 P 向上滑至点 M 处时,点 A 在相对于(1)的情况下向左移动的距离是多少?
(结果精确到 0.01cm,参考数据![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某空调厂的装配车间计划组装9000台空调.
(1)从组装空调开始,每天组装的台数m(单位:台/天)与生产时间t(单位:天)之间有怎样的函数关系?
(2)原计划用2个月时间(每月以30天计算)完成,由于气温提前升高,厂家决定这批空调提前10天上市,那么原装配车间每天至少要组装多少台空调?
查看答案和解析>>
科目:初中数学 来源: 题型:
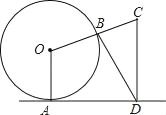
【题目】如图,直线l与⊙O相切于点A,作半径OB并延长至点C,使得BC=OB,作CD⊥直线l于点D,连接BD得∠CBD=75°,则∠OCD=_____度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O与AC相切于点A,且AB=AC,BC与⊙O相交于点D,下列说法不正确的是().
A. ∠C = 45° B. CD=BD C. ∠BAD=∠DAC D. CD=AB
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)已知∠MAN=135°,正方形ABCD绕点A旋转.
(1)当正方形ABCD旋转到∠MAN的外部(顶点A除外)时,AM,AN分别与正方形ABCD的边CB,CD的延长线交于点M,N,连接MN.
①如图1,若BM=DN,则线段MN与BM+DN之间的数量关系是 ;
②如图2,若BM≠DN,请判断①中的数量关系是否仍成立?若成立,请给予证明;若不成立,请说明理由;
(2)如图3,当正方形ABCD旋转到∠MAN的内部(顶点A除外)时,AM,AN分别与直线BD交于点M,N,探究:以线段BM,MN,DN的长度为三边长的三角形是何种三角形,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com