
【题目】如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P, AC=PC,∠COB=2∠PCB.
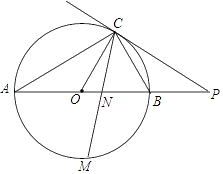
(1)求证:PC是⊙O的切线;
(2)求证:BC=![]() AB;
AB;
(3)点M是弧AB的中点,CM交AB于点N,若AB=8,求MN·MC的值.
【答案】(1)见解析;(2)见解析;(3)32
【解析】
(1)已知C在圆上,故只需证明OC与PC垂直即可;根据圆周角定理,易得∠PCB+∠OCB=90°,即OC⊥CP;故PC是⊙O的切线;
(2)AB是直径;故只需证明BC与半径相等即可;
(3)连接MA,MB,由圆周角定理可得∠ACM=∠BCM,进而可得△MBN∽△MCB,故BM2=MNMC;代入数据可得MNMC=BM2=8.
(1)证明:∵OA=OC,
∴∠A=∠ACO
又∵∠COB=2∠A,∠COB=2∠PCB,
∴∠A=∠ACO=∠PCB.
又∵AB是⊙O的直径
∴∠ACO+∠OCB=90°.
∴∠PCB+∠OCB=90°.
即OC⊥CP,
∵OC是⊙O的半径.
∴PC是⊙O的切线.
(2)证明:∵AC=PC,
∴∠A=∠P,
∴∠A=∠ACO=∠PCB=∠P.
又∵∠COB=∠A+∠ACO,∠CBO=∠P+∠PCB,
∴∠COB=∠CBO,
∴BC=OC.
![]()
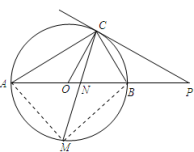
(3)解:连接MB,MA
∵点M是![]() 的中点,
的中点,
∴∠ACM=∠BCM.
∵∠ACM=∠ABM,
∴∠BCM=∠ABM.
又∵∠BMN=∠CMB,
∴△MBN∽△MCB.
∴![]()
∴![]()
又∵AB是⊙O的直径,![]()
∴∴∠AMB=90°,AM=BM.
∵AB=8,
∴![]()
∴![]()


科目:初中数学 来源: 题型:
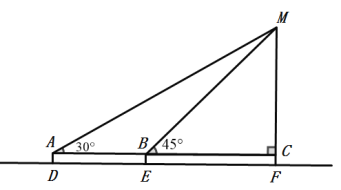
【题目】某校九年级数学兴趣小组的学生进行社会实践活动时,想利用所学的解直角三角形的知识测量教学楼的高度,他们先在点D处用测角仪测得楼顶M的仰角为30°,再沿DF方向前行40米到达点E处,在点E处测得楼顶M的仰角为45°,已知测角仪的高AD为1.5米,请根据他们的测量数据求此楼MF的高(结果精确到0.1m,参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,AC是对角线,今有较大的直角三角板,一边始终经过点B,直角顶点P在射线AC上移动,另一边交DC于点Q.
(1)如图①,当点Q在DC边上时,猜想并写出PB与PQ所满足的数量关系,并加以证明;
(2)如图②,当点Q落在DC的延长线上时,猜想并写出PB与PQ满足的数量关系,并证明你的猜想.

查看答案和解析>>
科目:初中数学 来源: 题型:
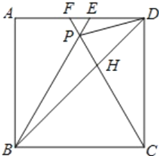
【题目】如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连结BD、DP,BD与CF相交于点H.给出下列结论,其中正确结论的个数是( )
①△BDE∽△DPE;②![]() ;③
;③![]() ;④tan∠DBE=
;④tan∠DBE=![]() .
.
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为庆祝中华人民共和国成立70周年,深圳举办了灯光秀,某数学兴趣小组为测量“平安金融中心”AB的高度,他们在地面C处测得另一幢大厦DE的顶部E处的仰角为32°,测得“平安中心”AB的顶部A处的仰角为44°.登上大厦DE的顶部E处后,测得“平安中心”AB的顶部A处的仰角为60°,(如图).已知C、D、B三点在同一水平直线上,且CD=400米,求平安金融中心AB的高度.(参考数据:sin32°≈0.53,cos32°≈0.85,tan32°≈0.62,tan44°≈0.99,![]() 1.41,
1.41,![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(教材呈现)下图是华师版九年级上册数学教材第78页的部分内容.
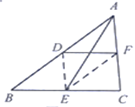
例1 求证:三角形的一条中位线与第三边上的中线互相平分.
已知:如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() .
.
求证:![]() 、
、![]() 互相平分.
互相平分.
证明:连结![]() 、
、![]() .
.
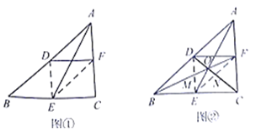
请根据教材提示,结合图①,写出完整的解题过程.
(结论应用)如图②,连结图①的![]() 、
、![]() ,分别与
,分别与![]() 、
、![]() 、
、![]() 交于点
交于点![]() 、
、![]() 、
、![]() .
.
(1)若![]() ,求点
,求点![]() 、
、![]() 之间的距离.
之间的距离.
(2)若四边形![]() 的面积为2,则
的面积为2,则![]() 的面积为______.
的面积为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
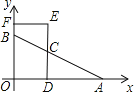
【题目】如图,在平面直角坐标系中,点A、B的坐标分别为(4,0)、(0,2),点C为线段AB上任意一点(不与点A、B重合).CD⊥OA于点D,点E在DC的延长线上,EF⊥y轴于点F,若点C为DE中点,则四边形ODEF的周长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
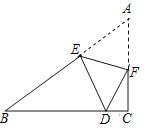
【题目】如图在Rt△ABC中,∠ACB=90°,AC=3,BC=4,点E、F分别在边AB、AC上,将△AEF沿直线EF折叠,使点A的对应点D恰好落在边BC上.若△BDE是直角三角形,则CF的长为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com