
 已知:如图,△ABC、△ADE都是等边三角形,求证:BE=CD.
已知:如图,△ABC、△ADE都是等边三角形,求证:BE=CD. 分析 由等边三角形的性质得出AB=AC,∠BAC=∠EAD=60°,AE=AD,得出∠BAE=∠CAD,由SAS证明△ABE≌△ACD,得出对应边相等即可.
解答 证明:∵△ABC、△ADE都是等边三角形,
∴AB=AC,∠BAC=∠EAD=60°,AE=AD,
∴∠BAE=∠CAD,
在△ABE和△ACD中,
$\left\{\begin{array}{l}{AB=AC}&{\;}\\{∠BAE=∠CAD}&{\;}\\{AE=AD}&{\;}\end{array}\right.$,
∴△ABE≌△ACD(SAS),
∴BE=CD.
点评 本题考查了等边三角形的性质、全等三角形的判定与性质;熟练掌握等边三角形的性质,证明三角形全等是解决问题的关键.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案科目:初中数学 来源: 题型:解答题
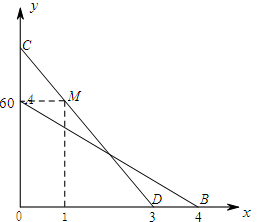 如图,线段AB、CD分别是一辆轿车和一辆客车在行驶过程中油箱内的剩余油量y1(升)、y2(升)关于行驶时间x(小时)的函数图象.
如图,线段AB、CD分别是一辆轿车和一辆客车在行驶过程中油箱内的剩余油量y1(升)、y2(升)关于行驶时间x(小时)的函数图象.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3-2=-9 | B. | -0.000000137=-1.37×107 | ||
| C. | (a2)-3=$\frac{1}{{a}^{6}}$ | D. | -$\frac{x-1}{x-y}$=$\frac{x+1}{x-y}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{x}$+$\sqrt{2x}$=$\sqrt{3x}$ | B. | 3$\sqrt{2}$-2$\sqrt{2}$=1 | C. | 2+$\sqrt{5}$=2$\sqrt{5}$ | D. | 2$\sqrt{2}$-$\sqrt{2}$=$\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com