
【题目】我们知道,三角形的三条角平分线交于一点,这个点称为三角形的内心(即三角形内切圆的圆心) . 现在规定,如果四边形的四条角平分线交于一点,我们把这个点称为“四边形的内心”.
问题提出
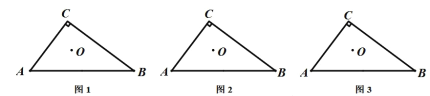
(1)如图1,在△ABC中,∠C=90°,点O为△ABC的内心,若直线DE分别交边AC、BC于点D、E,且点O仍然为四边形ABED的内心,这样的直线DE可以画多少条?请在图1中画出一条符合条件的直线DE,并简要说明画法.
问题探究
(2)如图2,在△ABC中,∠C=90°, AC=3, BC=4,若满足(1)中条件的一条直线DE // AB,求此时线段DE的长;
问题解决
(3)如图3,在△ABC中,∠C=90°, AC=3,BC=4,问满足(1)中条件的线段DE是否存在最小值?如果存在,请求出这个值;如果不存在,请说明理由.
【答案】(1)如图1,这样的直线DE可以画无数条;说明画法见解析;(2)DE=![]() ;(3)存在,DE有最小值2
;(3)存在,DE有最小值2![]() -2.
-2.
【解析】
(1)在AC上取点D,连接OD,作∠ODA'=∠ODA,DA'与BC交于点E,通过角平分线的性质定理和逆定理分析判断即可得到直线DE即为所求,所以这样的直线DE有无数条;
(2)由DE // AB,得到△CDE∽△CAB,通过题中数据计算即可;
(3)先求出∠DOE= 45°,然后作△ODE的外接圆⊙O',作O'G⊥DE于点G,连接O'O,O'D, O'E,通过O'O+O'G≥ON,即可得到DE的最小值.
解:(1) 如图1,这样的直线DE可以画无数条.
在AC上取点D,连接OD,作∠ODA'=∠ODA,DA'与BC交于点E,
连接OC;如图2,作OP⊥AC于点P,OQ⊥AB于点Q,ON⊥DE于点N,
由角平分线可知OP=ON=OM,故OE也为∠DEM的平分线,所以直线DE即为所求.
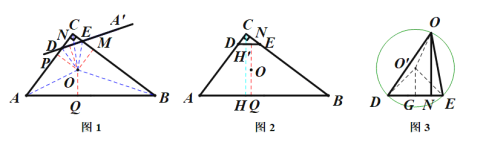
(2)在图1中,由DE//AB,可知N、O、Q共线;作CH⊥AB于点H,交DE于点H'.
由![]() AC·OP+
AC·OP+![]() BC·OM +
BC·OM +![]() AB·OQ=
AB·OQ=![]() AC·BC,有ON =OQ=OM=OP=l;
AC·BC,有ON =OQ=OM=OP=l;
由DE // AB,有∠CDE=∠CAB,∠CED=∠CBA ,
从而△CDE∽△CAB,
故![]() ,
,
即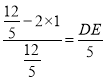 ,
,
解得DE=![]() .
.
(3)存在.
图1中,易知四边形OPCM是正方形,△ODP≌△ODN , △OEM≌△OEN ,
从而可知∠DOE=![]() ∠POM= 45°.
∠POM= 45°.
如图3,作△ODE的外接圆⊙O',作O'G⊥DE于点G,连接O'O,O'D, O'E;
由∠DO'E=2∠DOE=90°,有O'O=O'D=![]() ,O'G=
,O'G=![]() ;
;
由O'O+O'G≥ON,有![]() +
+![]() ≥1,解得DE≥2
≥1,解得DE≥2![]() -2,
-2,
∴DE有最小值2![]() -2.
-2.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线G:y=mx2+2mx+m﹣1(m≠0)与y轴交于点C,抛物线G的顶点为D,直线:y=mx+m﹣1(m≠0).

(1)当m=1时,画出直线和抛物线G,并直接写出直线被抛物线G截得的线段长.
(2)随着m取值的变化,判断点C,D是否都在直线上并说明理由.
(3)若直线被抛物线G截得的线段长不小于2,结合函数的图象,直接写出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD的对角线AC、BD相交于点O,AE平分∠BAD,分别交BC、BD于点E、P,连接OE,∠ADC=60°,AB=![]() BC=1,则下列结论:
BC=1,则下列结论:
①∠CAD=30°②BD=![]() ③S平行四边形ABCD=ABAC④OE=
③S平行四边形ABCD=ABAC④OE=![]() AD⑤S△APO=
AD⑤S△APO=![]() ,正确的个数是( )
,正确的个数是( )

A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校组织了一次体育测试,测试项目有A“立定跳远”、B“掷实心球”、C“仰卧起坐”、D“100米跑”、E“800米跑”.规定:每名学生测试三项,其中A、B为必测项目,第三项在C、D、E中随机抽取,每项10分(成绩均为整数且不低于0分).
(1)完成A、B必测项目后,用列表法,求甲、乙两同学第三项抽取不同项目的概率;
(2)某班有6名男生抽到了E“800米跑”项目,他们的成绩分别(单位:分)为:x,6,7,8,8,9.
①已知这组成绩的平均数和中位数相等,且x不是这组成绩中最高的,则x= ;
②该班学生丙因病错过了测试,补测抽到了E“800米跑”项目,加上丙同学的成绩后,发现这组成绩的众数与中位数相等,但平均数比原来的平均数小,则丙同学“800米跑”的成绩为多少?;
甲 乙 | |||
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次防流感知识检测中,学生得分均为整数,满分10分,成绩达到9分为优秀,这次检测中甲、乙两组学生人数相同,成绩如下两个统计图:
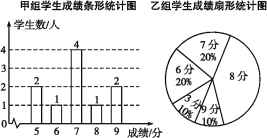
(1)在乙组学生成绩统计图中,8分所在的扇形的圆心角为 度;
(2)请列式计算乙组平均分,补充完整下面的成绩统计分析表所有空格:
平均分 | 方差 | 众数 | 中位数 | 优秀率 | |
甲组 | 7 | 1.8 | 7 | 7 | 20% |
乙组 | 2.6 | 10% |
(3)甲组学生说他们的优秀率高于乙组,所以他们的成绩好于乙组,但乙组学生不同意甲组学生的说法,认为他们组的成绩要好于甲组,请你给出两条支持乙组学生观点的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
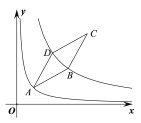
【题目】如图,菱形ABCD顶点A在例函数y=![]() (x>0)的图象上,函数 y=
(x>0)的图象上,函数 y=![]() (k>3,x>0)的图象关于直线AC对称,且经过点B、D两点,若AB=2,∠DAB=30°,则k的值为______.
(k>3,x>0)的图象关于直线AC对称,且经过点B、D两点,若AB=2,∠DAB=30°,则k的值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家推行“节能减排,低碳经济”政策后,低排量的汽车比较畅销,某汽车经销商购进A、B两种型号的低排量汽车,其中A型汽车的进货单价比B型汽车的进货单价多2万元;花50万元购进A型汽车的数量与花40万元购进B型汽车的数量相同.
(1)求A、B两种型号汽车的进货单价;
(2)销售中发现A型汽车的每周销量yA(台)与售价x(万元/台)满足函数关系yA=﹣x+20,B型汽车的每周销量yB(台)与售价x(万元/台)满足函数关系yB=﹣x+14,A型汽车的售价比B型汽车的售价高2万元/台.问A、B两种型号的汽车售价各为多少时,每周销售这两种汽车的总利润最大?最大利润是多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为丰富学生的校园生活,准备一次性购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),若购买3个足球和2个篮球共需170元,购买2个足球和5个篮球共需260元.
(1)购买一个足球、一个篮球各需多少元?(提示:列方程组解答)
(2)根据该中学的实际情况,需一次性购买足球和篮球共46个,要求购买足球和篮球的总费用不超过1480元,这所中学最多可以购买多少个篮球?(提示:列不等式解答)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市场将进货价为40元/件的商品按60元/件售出,每星期可卖出300件.市场调查反映:如调整价格,每涨价1元/件,每星期该商品要少卖出10件.
(1)请写出该商场每月卖出该商品所获得的利润y(元)与该商品每件涨价x(元)间的函数关系式;
(2)每月该商场销售该种商品获利能否达到6300元?请说明理由;
(3)请分析并回答每件售价在什么范围内,该商场获得的月利润不低于6160元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com