
【题目】已知二次函数y=-x2+(m+1)x-m(m为常数).
(1)求证:不论m为何值,该二次函数的图像与x轴总有公共点;
(2)若该二次函数的图像与x轴交于不同的两点A、B,与y轴交于点C,且AB2=2OC2(O为坐标原点),求m的值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
根据抛物线与x轴有交点时y=0,得到b2-4ac≥0,即可得出答案;
当y=0时求出抛物线与x轴的交点横坐标为m,1,求得AB的长,当x=0时,y=-m,求得 OC的长,再根据AB2=2OC2即可求出m.
(1)当y=0时,-x2+(m+1)x-m=0.
∵a=-1,b=(m+1) ,c=-m
∴b2-4ac=(m+1)2-4×(-1)×(-m)=(m-1)2≥0.
∴-x2+(m+1)x-m=0有实数解.
∴不论m为何值,该函数的图像与x轴总有公共点.
(2)当y=0时,-x2+(m+1)x-m=0.
∴x2-(m+1)x+m=0.
∴x1=m ,x2=1.
∴AB2=(m-1) 2.
当x=0时,y=-m.
∴OC2=(-m) 2.
∵AB2=2OC2,∴(m-1) 2=2 (-m) 2.
∴m1=-1+![]() ,m2=-1-
,m2=-1-![]() .
.
即m的值为-1+![]() 或-1-
或-1-![]() .
.


 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案科目:初中数学 来源: 题型:
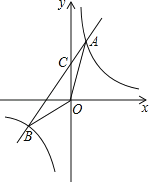
【题目】如图,直线y1=﹣x+4,y2=![]() x+b都与双曲线y=
x+b都与双曲线y=![]() 交于点A(1,m),这两条直线分别与x轴交于B,C两点.
交于点A(1,m),这两条直线分别与x轴交于B,C两点.
(1)求y与x之间的函数关系式;
(2)直接写出当x>0时,不等式![]() x+b>
x+b>![]() 的解集;
的解集;
(3)若点P在x轴上,连接AP把△ABC的面积分成1:3两部分,求此时点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周末,小李8时骑自行车从家里出发,到野外郊游,16时回到家里.他离家的距离s(千米)与时间t(时)之间的关系可以用图中的折线表示.现有如下信息:
①小李到达离家最远的地方是14时;
②小李第一次休息时间是10时;
③11时到12时,小李骑了5千米;
④返回时,小李的平均速度是10千米/时.
其中,正确的有( )
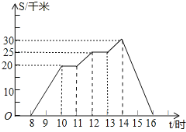
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=-2(x-1)(x-m+3)(m为常数),则下列结论正确的有( )
①抛物线开口向下; ②抛物线与y轴交点坐标为(0,-2m+6);
③当x<1时,y随x增大而增大;④抛物线的顶点坐标为(![]() ,
,![]() ).
).
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,小明将一张长为4、宽为3的矩形纸片沿对角线剪开,得到两张三角形纸片(如图2),将这两张三角纸片摆成如图3的形状,但点B、C、F、D在同一条直线上,且点C与点F重合(在图3至图6中统一用点F表示).
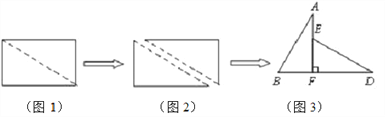
小明在对这两张三角形纸片进行如下操作时遇到了三个问题,请你帮助解决.
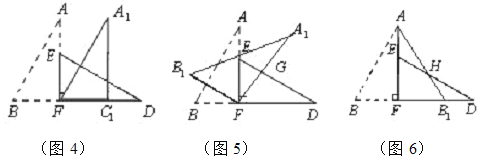
(1)将图3中的△ABF沿BD向右平移到图4中![]() 的位置,其中点B与点F 重合,请你求出平移的距离 ;
的位置,其中点B与点F 重合,请你求出平移的距离 ;
(2)在图5中若∠GFD=60°,则图3中的△ABF绕点 按 方向旋转 到图5的位置;
(3)将图3中的△ABF沿直线AF翻折到图6的位置,AB1交DE于点H,试问:△AEH和△HB1D的面积大小关系.说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
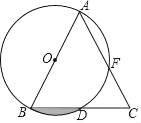
【题目】如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连结AC交⊙O于点F.
(1)AB与AC的大小有什么关系?请说明理由;
(2)若AB=8,∠BAC=45°,求:图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】不透明的口袋里装有红、黄、蓝三种颜色的小球若干个(除颜色外其余都相同),其中红球2个(分别标有1号、2号),蓝球1个.若从中任意摸出一个球,它是蓝球的概率为![]() .
.
(1)求袋中黄球的个数;
(2)第一次任意摸出一个球(不放回),第二次再摸出一个球,请用画树状图或列表格的方法,求两次摸到不同颜色球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y=kx+b的图象与反比例函数y=![]() 的图象交于A,B两点,点A的横坐标是2,点B的纵坐标是-2.
的图象交于A,B两点,点A的横坐标是2,点B的纵坐标是-2.
(1)求一次函数的解析式;
(2)求△AOB的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com