
【题目】某种贺卡原售价每张1元,甲商店这种贺卡七折优惠,而在乙商店这种贺卡除了八折优惠外,购买30张以上(含30张)免费送5张. 设一次买这种贺卡x张(x是正整数且30≤x≤50),若选择在甲商店购买需用y1元,若选择在乙商店购买需用y2元.
(1)假定你代购买45张这种贺卡,请确定应在哪一个商店买花钱较少;
(2)请分别写出y1(元)与x(张)、y2(元)与x(张)之间的函数关系式;
(3)在x的取值范围内,试讨论在哪一个商店买花钱较少.
【答案】(1)应选择在甲商店买贺卡花钱较少;
(2)y1=0.7x(30≤x≤50);y2=0.8x-4(35≤x≤50);
(3)当30≤x<35时,选择在甲商店买贺卡花钱较少;
当35≤x<40时,选择在乙商店买贺卡花钱较少;
当x=40时,甲乙商店任选一个;当40<x≤50时,选择在甲商店买贺卡花钱较少.
【解析】
(1)可分别计算出购买45张贺卡,甲乙两商店各需多少钱,然后比较哪个更省.
(2)本题要注意乙的表示方法要根据自变量的变化而变化.在甲商店购买的费用=打折后的单价×贺卡的张数,在乙商店购买的费用=打折后的单价×贺卡的张数(0-34张)或=打折后的单价×(贺卡的张数-获赠的张数)(35-50张).可根据此关系来得出y与x的关系式.
(3)要根据自变量的取值范围来分类讨论.
解:(1)当在甲商店购买45张贺卡时,用(0.7×45)=31.5元;
当在乙商店购买45张贺卡时,用[0.8×(45-5)]=32元.
∵31.5<32,
∴应选择在甲商店买贺卡花钱较少.
(2)根据题意,y1(元)与x(元)之间的函数关系式为y1=0.7x(30≤x≤50);
y2(元)与x(张)之间的函数关系式为y2=24(30≤x≤34)或y2=0.8(x-5),即y2=0.8x-4(35≤x≤50).
(3)根据题意,①当30≤x<35时,显然y1<y2;②当35≤x≤50时,令y1>y2;得
![]()
解得:35≤x<40. 令y1=y2,
得![]()
解得:x=40.
令y1<y2,得![]()
解得:40<x≤50.
答:当30≤x<35时,选择在甲商店买贺卡花钱较少;当35≤x<40时,选择在乙商店买贺卡花钱较少;当x=40时,甲乙商店任选一个;当40<x≤50时,选择在甲商店买贺卡花钱较少.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
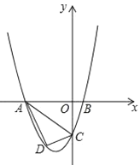
【题目】已知,如图抛物线![]() 与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.B的坐标为(1,0),且OC=4OB.
与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.B的坐标为(1,0),且OC=4OB.
(1)求点C坐标及抛物线的解析式;
(2)若点D是线段AC下方抛物线上的动点,求△ACD面积的最大值;
(3)若点E在x轴上,点P在抛物线上.是否存在以A,C,E,P为顶点且以AC为一边的平行四边形?若存在,直接写出P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
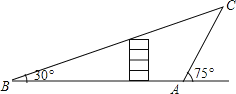
【题目】.如图,小明在大楼的东侧A处发现正前方仰角为75°的方向上有一热气球在C处,此时,小亮在大楼的西侧B处也测得气球在其正前方仰角为30°的位置上,已知AB的距离为60米,试求此时小明、小亮两人与气球的距离AC和BC.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c经过A(﹣6,0)、B(2,0)、C(0,6)三点,其顶点为D,连接AD,点P是线段AD上一个动点(不与A、D重合),过点P作y轴的垂线,垂足为点E,连接AE.
(1)求抛物线的函数解析式,并写出顶点D的坐标;
(2)如果点P的坐标为(x,y),△PAE的面积为S,求S与x之间的函数关系式,直接写出自变量x的取值范围,并求出S的最大值;
(3)过点P(﹣3,m)作x轴的垂线,垂足为点F,连接EF,把△PEF沿直线EF折叠,点P的对应点为点P,求出P的坐标.(直接写出结果)
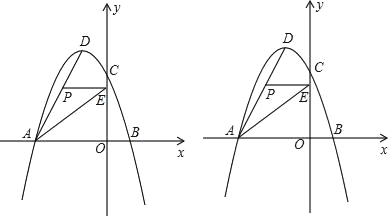
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)的顶点和该抛物线与y轴的交点在一次函数y=kx+1(k≠0)的图象上,它的对称轴是x=1.有下列四个结论,①. abc<0; ②. a<-![]() ;③. a=-k;④. 当0<x<1时,ax+b>k,其中正确结论的个数是( )
;③. a=-k;④. 当0<x<1时,ax+b>k,其中正确结论的个数是( )
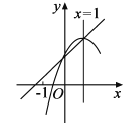
A.1;B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
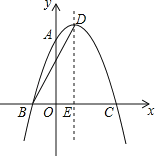
【题目】如图,抛物线y=ax2+2x+c经过点A(0,3),B(﹣1,0),请解答下列问题:
(1)求抛物线的解析式;
(2)抛物线的顶点为点D,对称轴与x轴交于点E,连接BD,求BD的长;
(3)点F在抛物线上运动,是否存在点F,使△BFC的面积为6,如果存在,求出点F的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图坐标系中,O(0,0),A(6,6![]() ),B(12,0),将△OAB沿直线CD折叠,使点A恰好落在线段OB上的点E处,若OE=
),B(12,0),将△OAB沿直线CD折叠,使点A恰好落在线段OB上的点E处,若OE=![]() ,则AC:AD的值是( )
,则AC:AD的值是( )
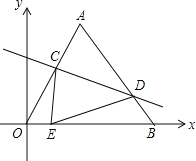
A.1:2B.2:3C.6:7D.7:8
查看答案和解析>>
科目:初中数学 来源: 题型:
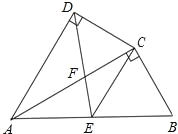
【题目】如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,
(1)求证:AC2=ABAD;
(2)求证:△AFD∽△CFE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() (
(![]() ,
,![]() 为常数).
为常数).
(1)当![]() ,
,![]() 时,求二次函数的最小值;
时,求二次函数的最小值;
(2)当![]() 时,若在函数值
时,若在函数值![]() 的情况下,只有一个自变量
的情况下,只有一个自变量![]() 的值与其对应,求此时二次函数的解析式;
的值与其对应,求此时二次函数的解析式;
(3)当![]() 时,若在自变量
时,若在自变量![]() 的值满足
的值满足![]() ≤
≤![]() ≤
≤![]() 的情况下,与其对应的函数值
的情况下,与其对应的函数值![]() 的最小值为21,求此时二次函数的解析式.
的最小值为21,求此时二次函数的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com