
科目:初中数学 来源: 题型:选择题
 在矩形ABCD中,AB=3,BC=1,E在AB上,AE=2,分别以E、B为圆心,以AE长为半径,画圆弧交DC于F、G,现向矩形ABCD区域内做投针试验,则投中阴影区域的概率为( )
在矩形ABCD中,AB=3,BC=1,E在AB上,AE=2,分别以E、B为圆心,以AE长为半径,画圆弧交DC于F、G,现向矩形ABCD区域内做投针试验,则投中阴影区域的概率为( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{2}{5}$ | D. | $\frac{π}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
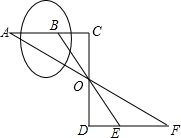 如图,某人要测量河中浅滩B和对岸A的距离,先在岸边定出点C,使C、A、B在一直线上,再在AC的垂直方向在岸边画线段CD,取它的中点O,又画DF⊥CD,观测E、O、B在一直线上,同时F、O、A也在一直线上,那么EF的长就是浅滩B和对岸A的距离,为什么?
如图,某人要测量河中浅滩B和对岸A的距离,先在岸边定出点C,使C、A、B在一直线上,再在AC的垂直方向在岸边画线段CD,取它的中点O,又画DF⊥CD,观测E、O、B在一直线上,同时F、O、A也在一直线上,那么EF的长就是浅滩B和对岸A的距离,为什么?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
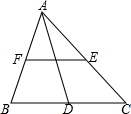 如图,EF为△ABC的中位线,AD为BC边上的中线.请从点A,B,C,D,E,F中选出四个点,使以这四个点为顶点的四边形为平行四边形(要求至少找出三个平行四边形).
如图,EF为△ABC的中位线,AD为BC边上的中线.请从点A,B,C,D,E,F中选出四个点,使以这四个点为顶点的四边形为平行四边形(要求至少找出三个平行四边形).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com