
���� ��1��������������������ȡ����ʽ�ֽ���ʽ���ɣ�
��2���ɷֽ�Ĺ���ֱ�ӵó��𰸼��ɣ�
��3����ʽ�ӳ�4-1���ٰѼ�������$\frac{1}{3}$���ɣ�
��� �⣺��1��x5-1
=x5-x+x-1
=x��x4-1��+x-1
=x��x-1����x3+x2+x+1��+��x-1��
=��x-1��[x��x3+x2+x+1��+1]
=��x-1����x4+x3+x2+x+1����
��2��xn-1=��x-1����xn-1+xn-2+��+x2+x+1����
��3��45+44+43+42+4+1
=��4-1����45+44+43+42+4+1����$\frac{1}{3}$
=��46-1����$\frac{1}{3}$
=$\frac{{4}^{6}-1}{3}$��
���� ���⿼����ʽ�ֽ��ʵ�����ã��������⣬���շֲ���ȡ����ʽ������ȵķ����ǽ������Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
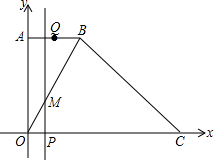 ��ͼ����ƽ��ֱ������ϵ�У���֪A��0��4����B��2��4������C��x����������ϣ��ҡ�BCO=45�㣬����OB������Q��ÿ��1����λ���ȵ��ٶȣ��ӵ�B������B-A-O���O�˶���ͬʱ����P����ͬ���ٶȣ��ӵ�O���߶�OC���C�˶�������P��ֱ��PM��OC��������O-B-C�ཻ�ڵ�M��������һ�㵽���յ�ʱ����һ��Ҳ��ֹ֮ͣ�˶������P�˶�ʱ��Ϊt���룩��
��ͼ����ƽ��ֱ������ϵ�У���֪A��0��4����B��2��4������C��x����������ϣ��ҡ�BCO=45�㣬����OB������Q��ÿ��1����λ���ȵ��ٶȣ��ӵ�B������B-A-O���O�˶���ͬʱ����P����ͬ���ٶȣ��ӵ�O���߶�OC���C�˶�������P��ֱ��PM��OC��������O-B-C�ཻ�ڵ�M��������һ�㵽���յ�ʱ����һ��Ҳ��ֹ֮ͣ�˶������P�˶�ʱ��Ϊt���룩���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
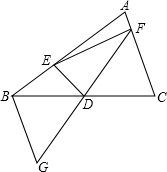 ��ͼ���ڡ�ABC�У�D��BC���е㣬����D��ֱ��GF��AC�ڵ�F����AC��ƽ����BG�ڵ�G��
��ͼ���ڡ�ABC�У�D��BC���е㣬����D��ֱ��GF��AC�ڵ�F����AC��ƽ����BG�ڵ�G���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
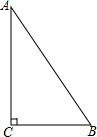 ��֪����ͼ��ʾ����Rt��ABC�У���C=90�㣬
��֪����ͼ��ʾ����Rt��ABC�У���C=90�㣬�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
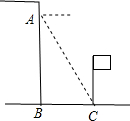 С���ڴ�¥����A���У����˵ײ�C�ĸ���Ϊ���ȣ����������߶�AB=h���ף�����ô��˵ײ����¥�ľ���BC=$\frac{h}{tan��}$�ף��æ������DZȺ�h��ʽ�ӱ�ʾ��
С���ڴ�¥����A���У����˵ײ�C�ĸ���Ϊ���ȣ����������߶�AB=h���ף�����ô��˵ײ����¥�ľ���BC=$\frac{h}{tan��}$�ף��æ������DZȺ�h��ʽ�ӱ�ʾ���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com