
【题目】某班“数学兴趣小组”对函数y=x2﹣2|x|的图象和性质进行了探究,探究过程如下,请补充完整.(1)自变量x的取值范围是全体实数,x与y的几组对应值列表如下:
x | … | ﹣3 | ﹣ | ﹣2 | ﹣1 | 0 | 1 | 2 |
| 3 | … |
y | … | 3 |
| m | ﹣1 | 0 | ﹣1 | 0 |
| 3 | … |
其中,m= .
(2)根据表中数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请画出该函数图象的另一部分.
(3)观察函数图象,写出两条函数的性质.
(4)进一步探究函数图象发现:
①函数图象与x轴有 个交点,所以对应的方程x2﹣2|x|=0有 个实数根;
②方程x2﹣2|x|=2有 个实数根.

③关于x的方程x2﹣2|x|=a有4个实数根时,a的取值范围是 .
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】学校开展捐书活动,以下是5名同学捐书的册数:4,9,5,x,3,已知这组数据的平均数是5,则这组数据的中位数和众数分别是( )
A. 3和3 B. 4和4 C. 3和4 D. 5和5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国中东部地区雾霾天气趋于严重,环境治理已刻不容缓.我市某电器商场根据民众健康需要,代理销售某种家用空气净化器,其进价是200元/台.经过市场销售后发现:在一个月内,当售价是400元/台时,可售出200台,且售价每降低10元,就可多售出50台.若供货商规定这种空气净化器售价不能低于300元/台,代理销售商每月要完成不低于450台的销售任务.
(1)试确定月销售量y(台)与售价x(元/台)之间的函数关系式;并求出自变量x的取值范围;
(2)当售价x(元/台)定为多少时,商场每月销售这种空气净化器所获得的利润w(元)最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填写下列解题过程中的推理根据:
已知:如图,点F、E分别在AB、CD上,AE、DF分别与BC相交于H、G,∠A=∠D,∠1+∠2=180°.说明:AB∥CD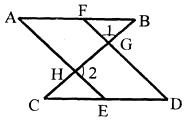
解:∵∠1=∠CGD()
∠1+∠2=180°
∴.
∴AE//FD ()
∴(两直线平行,同位角相等)
又∠A=∠D
∴∠D=∠BFD
∴()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平面直角坐标系xOy中,反比例函数![]() 的图象与一次函数y2=kx+b的图象交于点A(-4,-1)和点B(1,n).
的图象与一次函数y2=kx+b的图象交于点A(-4,-1)和点B(1,n).
(1)求这两个函数的表达式;
(2)观察图象,当y1>y2时,直接写出自变量x的取值范围;
(3)如果点C与点A关于y轴对称,求△ABC的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com