
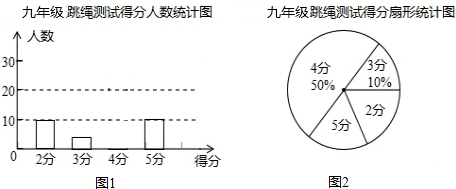
 小明上学期的数学成绩如表所示(单位:分)
小明上学期的数学成绩如表所示(单位:分)| 测验类别 | 平时 | 期中考试 | 期末考试 | |||
| 测试1 | 测试2 | 测试3 | 测试4 | |||
| 成绩 | 107 | 110 | 114 | 109 | 110 | 115 |
分析 (1)把6个数从小到大排列,按照中位数、众数的概念即可得出结论;
(2)把平时测试成绩相加,再求出其平均数即可;
(3)设其中、期末成绩各自所占的比例为x,y,列出关于x、y的方程组,求出xy的值即可.
解答 解:(1)这6个数从小到大排列为:107,109,110,110,114,115,中位数是110,众数是110.
故答案为:110,110;
(2)平时测试的数学平均成绩=$\frac{1}{4}$(107+110+114+109)=$\frac{1}{4}$×110=110(分);
(3)设其中、期末成绩各自所占的比例为x,y,
由题意得$\left\{\begin{array}{l}x+y=1-10%\\ 110x+115y+110×10%=113\end{array}\right.$,解得$\left\{\begin{array}{l}x=30%\\ y=60%\end{array}\right.$.
答:数学总评成绩中期中、期末成绩各自所占的比例分别为:30%,60%.
点评 本题考查的是扇形统计图,从扇形图上可以清楚地看出各部分数量和总数量之间的关系.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
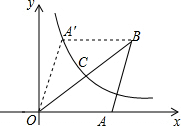 如图,在平面直角坐标系中,△OAB的边OA在x轴的正半轴上,OA=AB,边OB的中点C在双曲线y=$\frac{k}{x}$上,将△OAB沿OB翻折后,点A的对应点A′,正好落在双曲线y=$\frac{k}{x}$上,△OAB的面积为6,则k为( )
如图,在平面直角坐标系中,△OAB的边OA在x轴的正半轴上,OA=AB,边OB的中点C在双曲线y=$\frac{k}{x}$上,将△OAB沿OB翻折后,点A的对应点A′,正好落在双曲线y=$\frac{k}{x}$上,△OAB的面积为6,则k为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
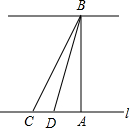 某市为了改善市区交通状况,计划修建一座新大桥,如图,新大桥的两端位于A、B两点,小张为了测量A、B之间的河宽,在垂直与新大桥AB的直线型道路l上测得如下数据:∠BDA=76.1°,∠BCA=68.2°,CD=82米.求AB的长(精确到0.1米,sin76.1°≈0.97,cos76.1°≈0.24,tan76.1°≈4.0;sin68.2°≈0.93,cos68.2°≈0.37,tan68.2°≈2.5.)
某市为了改善市区交通状况,计划修建一座新大桥,如图,新大桥的两端位于A、B两点,小张为了测量A、B之间的河宽,在垂直与新大桥AB的直线型道路l上测得如下数据:∠BDA=76.1°,∠BCA=68.2°,CD=82米.求AB的长(精确到0.1米,sin76.1°≈0.97,cos76.1°≈0.24,tan76.1°≈4.0;sin68.2°≈0.93,cos68.2°≈0.37,tan68.2°≈2.5.)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
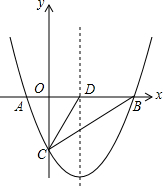 如图,抛物线y=$\frac{1}{2}$x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D.已知A(-1,0),C(0,-2).
如图,抛物线y=$\frac{1}{2}$x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D.已知A(-1,0),C(0,-2).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com