
����Ŀ����A��B����������������ʾ�����ֱ�Ϊa��b����A��B�����ľ���ɼ�Ϊ|a��b|��
��1����ͼ����A��B����������������ʾ�����ֱ�Ϊ��2��4����A��B����ľ���Ϊ��![]()
��2����A,B����ֱ���ÿ��3����λ���Ⱥ�ÿ��1����λ���ȵ��ٶ�ͬʱ�������������˶������˶�ʱ��Ϊt�룬����������⣺
���˶�t���A������ʾ����Ϊ �� B������ʾ����Ϊ�����𰸾��ú�t�Ĵ���ʽ��ʾ��
�ڵ�tΪ��ֵʱ��A��B����ľ���Ϊ4��
���𰸡�
��1��6
��2��3t��2,4+t,�⣺��A��B����ľ���Ϊ4,�ࣻ3t��2����t+4����=4�������ã�2t��6=��4����ã�t=1��t=5����t=1��t=5ʱ,A��B����ľ���Ϊ4
���������⣺��1��AB=|4������2��|=|6|=6��
�ʴ�Ϊ��6��
��2���ٵ�A��ʾ����Ϊ��2+3��t=3t��2����B��ʾ����Ϊ4+1��t=4+4��
�ʴ�Ϊ��3t��2��4+t��
��1��ץס��֪����A��B�����ľ���ɼ�Ϊ|a��b|�����뼴����������
��2����ץס��֪����A��B������˶��ٶȺ�������A��B�����λ�ü�������˶�t���Ӻ�A��B��������ʾ�������ڸ���AB=4����������ֵ������⼴�ɡ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��߳�����һ����ߣ����ſ��ƹ̶��ɱ������۴�����ԭ��ʹ����������ܹ�ȫ���۳������г����飬����ÿ�����280Ԫ����ʱ��ÿ�¿�����300���������۵���ÿ����1Ԫ��ÿ�¿ɶ��۳�2������ͳ�ƣ�ÿ����ߵĹ̶��ɱ�Q��Ԫ�����²�����y�������������¹�ϵ��

��1��д���²�����y�����������۵���x ��Ԫ��֮��ĺ�����ϵʽ��
��2����ÿ����ߵĹ̶��ɱ�Q��Ԫ�����²�����y������֮��ĺ�����ϵʽ��
��3����ÿ����ߵĹ̶��ɱ�Ϊ30Ԫ������ռ���۵��۵ļ���֮����
��4�����ó�������ߵ��²�����������400������ÿ����ߵĹ̶��ɱ�����Ϊ����Ԫ�����۵������Ϊ����Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�A��1��2����B��3��1����C����2����1����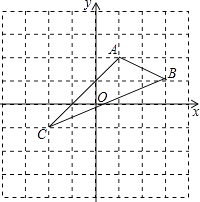
��1����ͼ��������ABC����y��ԳƵġ�A1B1C1 ��
��2��д��A1 �� B1 �� C1�����ֱ꣨��д���𰸣���
A1 ��B1 ��C1 ��
��3����A1B1C1�����Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB=AC��E��CA�ӳ����ϣ�AE=AF��AD�Ǹߣ����ж�EF��BC��λ�ù�ϵ����˵�����ɣ� 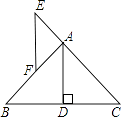
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����������y=![]() ��ͼ����ͼ��ʾ����һԪ���η���x2-��2k-1��x+k2-1=0��������ǣ� ��
��ͼ����ͼ��ʾ����һԪ���η���x2-��2k-1��x+k2-1=0��������ǣ� ��

A. û��ʵ�� B. ����������ʵ�� C. ���������ʵ�� D. ��ȷ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���ACB=90�㣬AC=BC��BE��CE��E��AD��CE��D�� 
��1����֤����ADC�ա�CEB��
��2��AD=5cm��DE=3cm����BE�ij��ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AD�ǡ�ABC�����ߣ�E��F�ֱ���AD��AD�ӳ����ϵĵ㣬��DE=DF������BF��CE������˵������CE=BF���ڡ�ABD�͡�ACD�����ȣ���BF��CE���ܡ�BDF�ա�CDE��������ȷ���У� �� 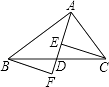
A.1��
B.2��
C.3��
D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѧ֮��������ϣ��ͬѧ�������⣨1������������������ټ���̽���о����⣨2����
��1����ͼ�٣���B=��C��BD=CE��AB=DC�� ����֤����ADEΪ���������Σ�
������B=60�㣬��֤����ADEΪ�ȱ������Σ�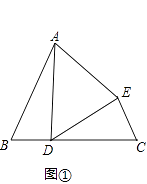
��2����ͼ�ڣ�����AM��BN��MA��AB��NB��AB����P��AB��һ�㣬������AM��BN�Ϸֱ�����C���� D ���㣺��CPDΪ����ֱ�������Σ���Ҫ������ֱ����Բ�棬��д������������ͼ�ۼ��� 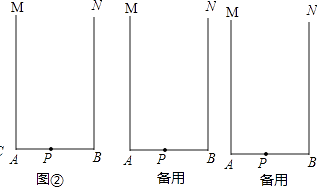
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com