
【题目】如图,在平面直角坐标系中,△CDE的顶点C点坐标为C(1,﹣2),点D的横坐标为![]() ,将△CDE绕点C旋转到△CBO,点D的对应点B在x轴的另一个交点为点A.
,将△CDE绕点C旋转到△CBO,点D的对应点B在x轴的另一个交点为点A.
(1)图中,∠OCE等于∠_____;
(2)求抛物线的解析式;
(3)抛物线上是否存在点P,使S△PAE=![]() S△CDE?若存在,直接写出点P的坐标;若不存在,请说明理由.
S△CDE?若存在,直接写出点P的坐标;若不存在,请说明理由.

【答案】(1)BCD;(2)y=![]() x2﹣x﹣
x2﹣x﹣![]() ;(3)存在;(1+
;(3)存在;(1+![]() ,1)或(1﹣
,1)或(1﹣![]() ,1)或(1+
,1)或(1+![]() ,﹣1)或(1﹣
,﹣1)或(1﹣![]() ,1).
,1).
【解析】
(1)根据旋转的性质易得∠OCE=∠BCD;
(2)(2)作CH⊥OE于H,如图,根据旋转的性质得CO=CE,CB=CD,OB=DE,则利用等腰三角形的性质得OH=HE=1,则E点坐标为(2,0),设B(m,0),D(![]() ,n),再利用两点间的距离公式求得m、n的值,然后设顶点式y=a(x-1)2-2,再把B点坐标代入求出a即可得到抛物线解析式;
,n),再利用两点间的距离公式求得m、n的值,然后设顶点式y=a(x-1)2-2,再把B点坐标代入求出a即可得到抛物线解析式;
(3)先利用抛物线的对称性得到A(-1,0),再根据旋转的性质得△CDE≌△CBO,则S△CDE=S△CBO=3,设P(t,![]() t2﹣t﹣
t2﹣t﹣![]() ),利用三角形面积公式得到关于t的方程,解关于t的一元二次方程求出t,从而可得到满足条件的P点坐标.
),利用三角形面积公式得到关于t的方程,解关于t的一元二次方程求出t,从而可得到满足条件的P点坐标.
解:(1)∵△CDE绕点C旋转到△CBO,
∴∠OCE=∠BCD;
故答案为BCD;
(2)作CH⊥OE于H,如图,
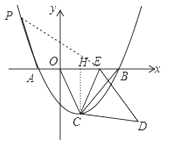
∵△CDE绕点C旋转到△CBO,
∴CO=CE,CB=CD,OB=DE,
∴OH=HE=1,
∴OE=2,
∴E点坐标为(2,0),
设B(m,0),D(![]() ,n),
,n),
∵CD2=(1﹣![]() )2+(﹣2﹣n)2 , CB2=(1﹣m)2+22 , DE2=(2﹣
)2+(﹣2﹣n)2 , CB2=(1﹣m)2+22 , DE2=(2﹣![]() )2+n2 ,
)2+n2 ,
∴(1﹣![]() )2+(﹣2﹣n)2=(1﹣m)2+22 , (2﹣
)2+(﹣2﹣n)2=(1﹣m)2+22 , (2﹣![]() )2+n2=m2 ,
)2+n2=m2 ,
∴m=3,n=﹣![]() ,
,
∴B(3,0),
设抛物线解析式为y=a(x﹣1)2﹣2,
把B(3,0)代入得4a﹣2=0,解得a=![]() ,
,
∴抛物线解析式为y=![]() (x﹣1)2﹣2,即y=
(x﹣1)2﹣2,即y=![]() x2﹣x﹣
x2﹣x﹣![]() ;
;
(3)存在.
A与点B关于直线x=1对称,
∴A(﹣1,0),
∵△CDE绕点C旋转到△CBO,
∴△CDE≌△CBO,
∴S△CDE=S△CBO=![]() 23=3,
23=3,
设P(t,![]() t2﹣t﹣
t2﹣t﹣![]() ),
),
∵S△PAE=![]() S△CDE ,
S△CDE ,
∴![]() 3|
3|![]() t2﹣t﹣
t2﹣t﹣![]() |=
|=![]() 3,
3,
∴![]() t2﹣t﹣
t2﹣t﹣![]() =1或
=1或![]() t2﹣t﹣
t2﹣t﹣![]() =﹣1,
=﹣1,
解方程![]() t2﹣t﹣
t2﹣t﹣![]() =1得t1=1+
=1得t1=1+![]() ,t2=1﹣
,t2=1﹣![]() ,此时P点坐标为(1+
,此时P点坐标为(1+![]() ,1)或(1﹣
,1)或(1﹣![]() ,1);
,1);
解方程![]() t2﹣t﹣
t2﹣t﹣![]() =﹣1得t1=1+
=﹣1得t1=1+![]() ,t2=1﹣
,t2=1﹣![]() ,此时P点坐标为(1+
,此时P点坐标为(1+![]() span>,﹣1)或(1﹣
span>,﹣1)或(1﹣![]() ,1);
,1);
综上所述,满足条件的P点坐标为(1+![]() ,1)或(1﹣
,1)或(1﹣![]() ,1)或(1+
,1)或(1+![]() ,﹣1)或(1﹣
,﹣1)或(1﹣![]() ,1).
,1).


科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c(a,b,c为常数)的对称轴为x=1,与y轴的交点为c(0,4),y的最大值为5,顶点为M,过点D(0,1)且平行于x轴的直线与抛物线交于点A,B.
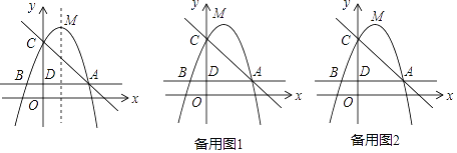
(Ⅰ)求该二次函数的解析式和点A、B的坐标;
(Ⅱ)点P是直线AC上的动点,若点P,点C,点M所构成的三角形与△BCD相似,求出所有点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场计划购进一批甲、乙两种玩具,已知一件甲种玩具的进价与一件乙种玩具的进价的和为40元,用90元购进甲种玩具的件数与用150元购进乙种玩具的件数相同.
(1)求每件甲种、乙种玩具的进价分别是多少元?
(2)商场计划购进甲、乙两种玩具共48件,其中甲种玩具的件数少于乙种玩具的件数,商场决定此次进货的总资金不超过1000元,求商场共有几种进货方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘海轮位于灯塔P的南偏东60方向,距离灯塔100海里的A处,它计划去往位于灯塔P的北偏东45方向上的B处.(参考数据![]() ≈1.414,
≈1.414, ![]() ≈1.732,
≈1.732, ![]() ≈2.449)
≈2.449)
(1)问B处距离灯塔P有多远?(结果精确到0.1海里)
(2)假设有一圆形暗礁区域,它的圆心位于射线PB上,距离灯塔190海里的点O处.圆形暗礁区域的半径为50海里,进入这个区域,就有触礁的危险.请判断海轮到达B处是否有触礁的危险,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
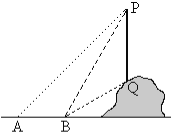
【题目】如图所示,某数学活动小组要测量山坡上的电线杆PQ的高度.他们采取的方法是:先在地面上的点A处测得杆顶端点P的仰角是45°,再向前走到B点,测得杆顶端点P和杆底端点Q的仰角分别是60°和30°,这时只需要测出AB的长度就能通过计算求出电线杆PQ的高度.你同意他们的测量方案吗?若同意,画出计算时的图形,简要写出计算的思路,不用求出具体值;若不同意,提出你的测量方案,并简要写出计算思路.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一次军事演习中,蓝方在一条东西走向的公路上的A处朝正南方向撤退,红方在公路上的B处沿南偏西60°方向前进实施拦截,红方行驶1000米到达C处后,因前方无法通行,红方决定调整方向,再朝南偏西45°方向前进了相同的距离,刚好在D处成功拦截蓝方,求拦截点D处到公路的距离(结果不取近似值).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B

(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=6![]() ,AF=4
,AF=4![]() ,求AE的长.
,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如果M个不同的正整数,对其中的任意两个数,这两个数的积能被这两个数的和整除,则称这组数为M个数的自然数组,如(3,6)为两个数的自然数组,因为(3×6)能被(3+6)整除;又如(15,30,60)为三个数的自然数组,因为(15×30)能被(15+30)整除,(15×60)能被(15+60)整除,(30×60)能被(30+60)整除…
(1)求证:2n和n(n﹣2)(n≥3,n为整数)组成的数组是两个数的自然数组;
(2)若(4a,5a,6a)是三个数的自然数组,求满足条件的三位正整数a,并判断(4a+5,5a+5,6a+5)是否为自然数组.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com