
 顶点的三角形与以D,E,F为顶点的三角形全等,求a,b的值.(只需写出结果,不必写出解答过程)
顶点的三角形与以D,E,F为顶点的三角形全等,求a,b的值.(只需写出结果,不必写出解答过程)
|
|
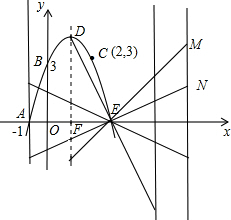
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 7 |
| 2 |
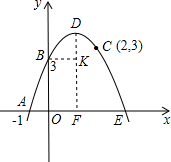
| DK2+BK2 |
| 2 |
| DF2+FE2 |
| 5 |
| 10 |
| 2 |
| 10 |
| 2 |
| 2 |
| 5 |
| AO |
| BD |
| BO |
| BE |
| AB |
| DE |
| 1 | ||
|
|
|
|
|
|
|
|


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| 1 |
| 2 |
| PQ |
| NP+BQ |

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 BC=80m,CD=40m,现计划在上面建设一个面积为S的矩形综合楼PMBN,其中点P在线段AD上,且PM的长至少为36m.
BC=80m,CD=40m,现计划在上面建设一个面积为S的矩形综合楼PMBN,其中点P在线段AD上,且PM的长至少为36m.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com