
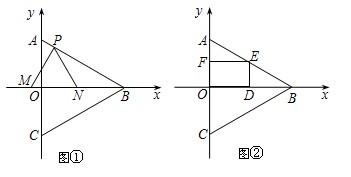
(1)如图所示,矩形ABCD的两条对角线相交于点O,∠AOD=120°,AB=6cm,求AC的长.

(2)如图所示,在四边形ABCD中,∠DAB=∠BCD=90°,O、M分别是AC、BD的中点,过点C作CN∥AM交MO的延长线于点N.
求证:四边形AMCN是菱形

|
(1) 解:因为四边形ABCD为矩形.所以 AC=BD,AO=BO=CO=DO.因为∠ A0D=120°,所以∠AOB=60°,所以△ AOB为等边三角形.所以 AO=AB=6cm,所以AC=2AO=12cm.(2) 证明:由AM∥CN,OA=OC,∠AOM=∠COM,得△AOM和△CON关于O点中心对称,所以AM=CN.又因AM∥CN,所以四边形AMCN是平行四边形,又在Rt△ABD中,AM是斜边BD上的中线,即得 .同理可得 .同理可得 ,故AM=CM,所以平行四边形AMCN是菱形. ,故AM=CM,所以平行四边形AMCN是菱形.
|
|
(1)矩形的两条对角线的夹角为60°,则矩形被对角线分成的四个三角形中有两个是等边三角形. 矩形的对角线把矩形分成了四个等腰三角形. (2)要证AMCN是菱形,首先看适合哪一种判定方法,题中已给出CN∥AM,而O又是AC的中点,得△AOM和△CON关于O点中少对称,得M=CN,即四边形AMCN是平行四边形.再证一组邻边相等是问题的关键,而AM、CM分别是Rt△ABC和Rt△BCD斜边BD上的中线,所以 应注意到四边形ABCD是由两个有公共斜边BD的直角三角形组成的.且AM、CM是它们公共斜边BD上的中线,因此AM=CM. |


科目:初中数学 来源: 题型:
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com