
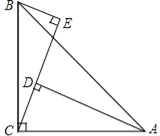
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D.
(1)求证:△ADC≌△CEB.
(2)AD=5cm,DE=3cm,求BE的长度.
【答案】(1)证明见解析;(2) 2cm.
【解析】试题分析:(1)根据同角的余角相等可得∠BCE=∠CAD,再由全等三角形的判定定理AAS即可判定△ADC≌△CEB;(2)利用(1)中的全等三角形的对应边相等得到:AD=CE=5cm,CD=BE.则根据图中相关线段的和差关系得到BE=AD-DE,即可求得BE的长度.
试题解析:(1)证明:如图,∵AD⊥CE,∠ACB=90°,
∴∠ADC=∠ACB=90°,
∴∠BCE=∠CAD(同角的余角相等).
在△ADC与△CEB中,
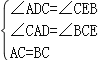 ,
,
∴△ADC≌△CEB(AAS);
(2)由(1)知,△ADC≌△CEB,则AD=CE=5cm,CD=BE.
如图,∵CD=CE﹣DE,
∴BE=AD﹣DE=5﹣3=2(cm),即BE的长度是2cm.


科目:初中数学 来源: 题型:
【题目】团队游客年龄的方差分别是S甲2=1.4,S乙2=18.8,S丙2=2.5,导游小力最喜欢带游客年龄相近龄的团队,则他在甲、乙、丙三个的中应选_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】寻找公式,求代数式的值:从2开始,连续的偶数相加,它们的和的情况如下表:

(1)当n个从2开始的连续偶数相加时,它们的和S与n之间有什么样的关系,用公式表示出来;
(2)并按此规律计算:(a)2+4+6+…+400的值; (b)162+164+166+…+300的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】古希腊数学家把1,3,6,10,15,21叫做三角数,它有一定的规律性,若把第一个三角数记为a1,第二个三角数记为a2,, 第n个三角数记为an,计算a1+a2,a2+a3,a3+a4,,由此推算a199+a200的值为( )
A. 20000 B. 40000 C. 39701 D. 19701
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品原价为每件x元,第一次降价是打“八折”(即按原价的80%)出售,第二次降价又减少10元,这时该商品的售价是_____元.(用含x的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下各组线段为边,能组成三角形的是( )
A.2cm,4cm,6cm
B.8cm,6cm,4cm
C.14cm,6cm,7cm
D.2cm,3cm,6em
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com