
【题目】阅读理解:
(问题情境)
教材中小明用4张全等的直角三角形纸片拼成图1,利用此图,可以验证勾股定理吗?


(探索新知)
从面积的角度思考,不难发现:大正方形的面积=小正方形的面积 + 4个直角三角形的面积,从而得数学等式: ;(用含字母a、b、c的式子表示)化简证得勾股定理:![]()
(初步运用)
(1)如图1,若b=2a ,则小正方形面积:大正方形面积= ;
(2)现将图1中上方的两直角三角形向内折叠,如图2,若a= 4,b= 6此时空白部分的面积为 ;
(迁移运用)
如果用三张含60°的全等三角形纸片,能否拼成一个特殊图形呢?带着这个疑问,小丽拼出图3的等边三角形,你能否仿照勾股定理的验证,发现含60°的三角形三边a、b、c之间的关系,写出此等量关系式及其推导过程.
知识补充:如图4,含60°的直角三角形,对边y :斜边x=定值k
【答案】[探索新知]:![]() ;[初步运用]:(1)5:9;(2)28; [迁移运用] :
;[初步运用]:(1)5:9;(2)28; [迁移运用] :![]() ,证明详见解析.
,证明详见解析.
【解析】
[探索新知]
分别表示出大正方形,小正方形,直角三角形面积,再由面积关系可得关系式;
[初步运用]
(1)将b=2a代入![]() 可推出
可推出![]() ,即小正方形面积为
,即小正方形面积为![]()
大正方形面积=![]() ,可求出比值;
,可求出比值;
(2)空白部分面积为小正方形面积减去2个直角三角形面积;
[迁移运用]
大正三角形面积=三个全等三角形面积+小正三角形面积,分别求出面积代入关系式化简即可.
[探索新知]
大正方形边长为![]() ,所以面积=
,所以面积=![]() ,小正方形的边长为
,小正方形的边长为![]() ,所以面积=
,所以面积=![]() ,
,
直角三角形的面积=![]() ,由大正方形的面积=小正方形的面积 + 4个直角三角形的面积可得
,由大正方形的面积=小正方形的面积 + 4个直角三角形的面积可得![]()
[初步运用]
(1)将b=2a代入![]() 得
得![]() ,∴
,∴![]() ,即小正方形面积为
,即小正方形面积为![]()
大正方形面积=![]() ,
,
∴ 小正方形面积:大正方形面积=![]() :
:![]() =5:9
=5:9
(2)∵a= 4,b= 6
∴小正方形面积=![]() ,直角三角形面积=
,直角三角形面积=![]()
∴空白部分面积=小正方形面积-两个直角三角形面积=![]()
[迁移运用]
由补充知识可得大正三角形的高为![]() ,小正三角形的高为
,小正三角形的高为![]() ,全等三角形的高为
,全等三角形的高为![]() ,则由大正三角形面积=三个全等三角形面积+小正三角形面积可得
,则由大正三角形面积=三个全等三角形面积+小正三角形面积可得
![]()
![]()
∴![]()


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源: 题型:
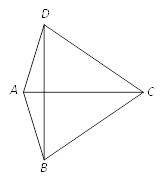
【题目】如图,在四边形ABCD中,AB=AD,AC是∠BAD的角平分线.
(1)求证:△ABC≌△ADC.
(2)若∠BCD=60°,AC=BC,求∠ADB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,经过原点O的抛物线![]() 与x轴交于另一点
与x轴交于另一点![]() ,在第一象限内与直线
,在第一象限内与直线![]() 交于点
交于点![]() .
.
![]() 求这条抛物线的表达式;
求这条抛物线的表达式;
![]() 在第四象限内的拋物线上有一点C,满足以B,O,C为顶点的三角形的面积为2,求点C的坐标;
在第四象限内的拋物线上有一点C,满足以B,O,C为顶点的三角形的面积为2,求点C的坐标;
![]() 如图2,若点M在这条抛物线上,且
如图2,若点M在这条抛物线上,且![]() ,
,
![]() 求点M的坐标;
求点M的坐标;
![]() 在
在![]() 的条件下,是否存在点P,使得
的条件下,是否存在点P,使得![]() ∽
∽![]() ?若存在,求出点P的坐标;若不存在,请说明理由.
?若存在,求出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 经过点A(
经过点A(![]() ,0),B(
,0),B(![]() ,0),且与y轴相交于点C.
,0),且与y轴相交于点C.
(1)求这条抛物线的表达式;
(2)求∠ACB的度数;
(3)设点D是所求抛物线第一象限上一点,且在对称轴的右侧,点E在线段AC上,且DE⊥AC,当△DCE与△AOC相似时,求点D的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】暑假期间,两位家长计划带领若干名学生去旅游,他们联系了报价均为每人400元的两家旅行社.经协商,甲旅行社的优惠条件是:两位家长全额收费,学生都按七折收费;乙旅行社的优惠条件是:家长、学生都按八折收费假设这两位家长带领x名学生去旅游.
(1)如果设选择甲旅行社所用的费用为![]() 元,选择乙旅行社所用的费用为
元,选择乙旅行社所用的费用为![]() 元.请写出
元.请写出![]() 、
、![]() 与x的关系式.
与x的关系式.
(2)在(1)的前提下,请你帮助两位家长根据所带学生人数,选择哪家旅行社合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四幅图象分别表示变量之间的关系,请按图象的顺序,将下面的四种情境与之对应排序.正确的顺序是( )

①篮球运动员投篮时,投出去的篮球的高度与时间的关系
②去超市购买同一单价的水果,所付费用与水果数量的关系
③李老师使用的是一种含月租的手机计费方式,则他每月所付话费与通话时间的关系
④周末,小明从家到图书馆,看了一段时间书后,按原速度原路返回,小明离家的距离与时间的关系
A. ①②③④ B. ①③④② C. ①③②④ D. ①④②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是一块锐角三角形材料,高线AH长8 cm,底边BC长10 cm,要把它加工成一个矩形零件,使矩形DEFG的一边EF在BC上,其余两个顶点D,G分别在AB,AC上,则四边形DEFG的最大面积为( )

A. 40 cm2 B. 20 cm2
C. 25 cm2 D. 10 cm2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com