
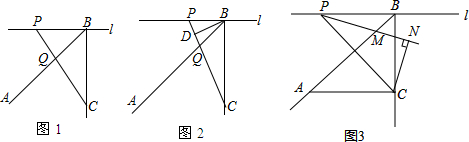
分析 (1)如图1中,作QE⊥PB,QF⊥BC垂足分别为E、F,由角平分线性质定理得QE=QF,再根据S△PBQ:S△BCQ=PQ:QC即可解决问题.
(2)如图2中,作CF⊥AB垂足为F交BD的延长线于E,构造了全等三角形△CFQ≌△BFE解决问题.
(3)证明Rt△ACB≌Rt△PBC,得到∠PCB=45°,在△PCN中,利用三角形的内角和为180°,即可解答.
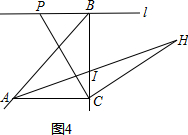
(4)如图4中,作HE⊥BC垂足为E,构造了全等三角形△PCB≌△CHE解决问题,注意当点P在直线l上移动时,点I在BC的延长线时的情形.
解答 解:(1)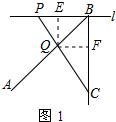 如图1中,作QE⊥PB,QF⊥BC垂足分别为E、F.
如图1中,作QE⊥PB,QF⊥BC垂足分别为E、F.
∵∠PBC=90°,∠ABC=45°,
∴∠ABC=∠ABP,
∴QE=QF,
∵S△PBQ:S△BCQ=PQ:QC,
∴$\frac{1}{2}$•PB•QE:$\frac{1}{2}$•BC•QF=PQ:QC,
∴PQ:QC=2:3,
即$\frac{PQ}{CQ}=\frac{2}{3}$.
(2)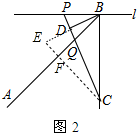 结论CQ=2BD,理由如下:
结论CQ=2BD,理由如下:
证明:如图2中,作CF⊥AB垂足为F交BD的延长线于E.
∵∠CFB=∠BFE=90°,∠ABC=45°,
∴∠FBC=∠FCB=45°,
∴FB=FC,
∵BD⊥CD,
∴∠BDQ=∠QFC=90°,
∵∠DQB=∠FQC,
∴∠DBQ=∠QCF,
在△CFQ和△BFE中,
$\left\{\begin{array}{l}{∠FCQ=∠EBF}\\{CF=BF}\\{∠CFQ=∠BFE}\end{array}\right.$,
∴△CFQ≌△BFE,
∴CQ=BE,
∵∠BPC=3∠C,∠C+∠BPC=90°,
∴∠PCB=∠FCQ=22.5°,
∴∠CBD=∠CED=67.5°,
∴CB=CE,
∵CD⊥EB,
∴DB=ED,
∴CQ=2BD.
(3)如图3,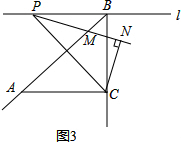
∵l⊥BC,AC⊥BC,
∴∠ACB=∠PBC=90°,
在Rt△ACB和Rt△PBC中,
$\left\{\begin{array}{l}{AB=PC}\\{BC=CB}\end{array}\right.$
∴Rt△ACB≌Rt△PBC,
∴∠ABC=∠PCB,
∵∠ABC=45°,
∴∠PCB=45°,
∵CN⊥PN,
∴∠PNC=90°,
∴在△PCN中,∠BCN=180°-∠CPN-∠PNC-∠PCB=180°-α-90°-45°=45°-α.
(4)如图4中,作HE⊥BC垂足为E.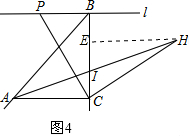
∵∠PCH=∠PBC=90°,
∴∠CPB+∠PCB=90°,∠PCB+∠HCE=90°,
∴∠CPB=∠HCE,
在△PCB和△CHE中
$\left\{\begin{array}{l}{∠CPB=∠HCE}\\{∠PBC=∠HEC}\\{CP=CH}\end{array}\right.$,
∴△PCB≌△CHE,
∴BC=EH,PB=EC,
∠ACB=90°,∠ABC=45°,
∴∠ABC=∠BAC=45°,
∴AC=BC=EH,
在△ACI和△HEI中,
$\left\{\begin{array}{l}{∠ACI=∠HEI}\\{∠AIC=∠EIH}\\{AC=EH}\end{array}\right.$,
∴△ACI≌△HEI,
∴EI=IC,
∴IC=BC-BI=AC-BI=m-n,
BP=2EI=2(m-n),
当点I在BC的延长线时,IC=BI-BC=BI-AC=n-m,BP=2IC=2(n-m).
综上所述:BP=2|m-n|.
故答案为2|m-n|.
点评 本题考查全等三角形的判定和性质、角平分线的性质定理,构造全等三角形是解决问题的关键,易错的地方是最后一个问题漏解,考虑问题要全面.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
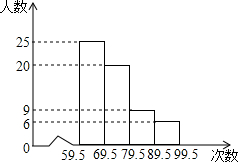 如图是九年级(1)班同学的一次体检每分钟心跳次数的频数分布直方图(次数均为整数).已知该班只有5位同学的心跳每分钟75次.请观察图回答:
如图是九年级(1)班同学的一次体检每分钟心跳次数的频数分布直方图(次数均为整数).已知该班只有5位同学的心跳每分钟75次.请观察图回答:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com