
【题目】将矩形ABCD绕点B顺时针旋转得到矩形A1BC1D1,点A、C、D的对应点分别为A1、C1、D1,当点A1落在AC上时.
(1)如图,若∠CAB=60°,求证:四边形ABD1C为平行四边形;
(2)如图,AD1交CB于点O.若∠CAB≠60°,求证:DO=AO.

【答案】(1)见解析;(2)见解析.
【解析】
(1)证△ABA1是等边三角形,得∠AA1B=∠A1BD1,由AC∥BD1,AC=BD1,可得;(2)连接BD1.证△BCD1≌D1A1B,得四边形ABD1C是平行四边形,再证△OCD1≌△OBA(AAS),△DCO≌△ABO(SAS),可得DO=OA.
证明:(1)如图1中,
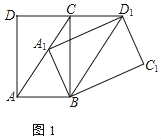
∵∠BAC=60°,BA=BA1,
∴△ABA1是等边三角形,
∴∠AA1B=60°,
∵∠A1BD1=60°,
∴∠AA1B=∠A1BD1,
∴AC∥BD1,
∵AC=BD1,
∴四边形ABD1C是平行四边形.
(2)如图2中,连接BD1.
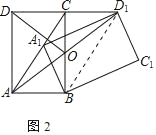
∵∠BCD1=∠BAD1=90°,BD1=D1B,BC=A1D1,
∴△BCD1≌D1A1B,
∴CD1=BA1,
∵BA=BA1,
∴AB=CD1,∵AC=BD1
∴四边形ABD1C是平行四边形,
∴CD1∥AB,CD1=AB,
∠OCD1=∠ABO,
∵∠COD1=∠AOB,
∴△OCD1≌△OBA(AAS),
∴OC=OB,
∵CD=BA,∠DCO=∠ABO,
∴△DCO≌△ABO(SAS),
∴DO=OA.


科目:初中数学 来源: 题型:
【题目】如图,有两个小机器人A、B在一条笔直的道路上由西向东行走,两机器人相距6cm,即AB=6cm.其中机器人A的速度为3cm/s,机器人B的速度为2cm/s.设机器人B行走的时间为t(s).
(1)若两机器人同时出发,
①当t=![]() 时,AB= cm;当t=7时,AB= cm;
时,AB= cm;当t=7时,AB= cm;
②当两机器人相距4cm时,求机器人B行走的时间t的值;
(2)若机器人B先行走2s,机器人A再行走,当两机器人相距10cm时,请直接写出t的值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
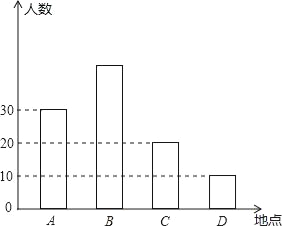
【题目】如图,暑假快要到了,某市准备组织同学们分别到A,B,C,D四个地方进行夏令营活动,前往四个地方的人数.
(1)去B地参加夏令营活动人数占总人数的40%,根据统计图求去B地的人数?
(2)若一对姐弟中只能有一人参加夏令营,姐弟俩提议让父亲决定.父亲说:现有4张卡片上分别写有1,2,3,4四个整数,先让姐姐随机地抽取一张后放回,再由弟弟随机地抽取一张.若抽取的两张卡片上的数字之和是5的倍数则姐姐参加,若抽取的两张卡片上的数字之和是3的倍数则弟弟参加.用列表法或树形图分析这种方法对姐弟俩是否公平?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“数形结合”是一种重要的数学思维,观察下面的图形和算式:
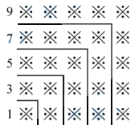
1=1=12
1+3=4=22
1+3+5=9=32
1+3+5+7=16=42
1+3+5+7+9=25=52
解答下列问题:请用上面得到的规律计算:21+23+25+27+…+101=( )
A.2601B.2501C.2400D.2419
查看答案和解析>>
科目:初中数学 来源: 题型:
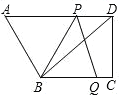
【题目】如图,在四边形ABCD中,AD//BC, ![]() ,BC=4,DC=3,AD=6.动点P从点D出发,沿射线DA的方向,在射线DA上以每秒2两个单位长的速度运动,动点Q从点C出发,在线段CB上以每秒1个单位长的速度向点B运动,点P、Q分别从点D,C同时出发,当点Q运动到点B时,点P随之停止运动.设运动的时间为t(秒).
,BC=4,DC=3,AD=6.动点P从点D出发,沿射线DA的方向,在射线DA上以每秒2两个单位长的速度运动,动点Q从点C出发,在线段CB上以每秒1个单位长的速度向点B运动,点P、Q分别从点D,C同时出发,当点Q运动到点B时,点P随之停止运动.设运动的时间为t(秒).
(1)设![]() 的面积为
的面积为![]() ,直接写出
,直接写出![]() 与
与![]() 之间的函数关系式是____________(不写取值范围).
之间的函数关系式是____________(不写取值范围).
(2)当B,P,Q三点为顶点的三角形是等腰三角形时,求出此时![]() 的值.
的值.
(3)当线段PQ与线段AB相交于点O,且2OA=OB时,直接写出![]() =_____________.
=_____________.
(4)是否存在时刻![]() ,使得
,使得![]() 若存在,求出
若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两个边长分别为a,b(a>b)的正方形连在一起,三点C,B,F在同一直线上,反比例函数y=![]() 在第一象限的图象经过小正方形右下顶点E.若OB2﹣BE2=8,则k的值是( )
在第一象限的图象经过小正方形右下顶点E.若OB2﹣BE2=8,则k的值是( )

A. 3 B. 4 C. 5 D. 4![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一张长方形纸片,![]() 长为
长为![]() ,
,![]() 长为
长为![]() .
.

(1)若将此长方形纸片绕它的一边所在直线旋转一周,则形成的几何体是______;
(2)若将这个长方形纸片绕![]() 边所在直线旋转一周,则形成的几何体的体积是____
边所在直线旋转一周,则形成的几何体的体积是____![]() (结果保留
(结果保留![]() );
);
(3)若将这个长方形纸片绕它的一边所在直线旋转一周,求形成的几何体的表面积(结果保留![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中xOy中,抛物线![]() 的顶点在x轴上.
的顶点在x轴上.
(1)求抛物线的表达式;
(2)点Q是x轴上一点,
①若在抛物线上存在点P,使得∠POQ=45°,求点P的坐标;
②抛物线与直线y=2交于点E,F(点E在点F的左侧),将此抛物线在点E,F(包含点E和点F)之间的部分沿x轴平移n个单位后得到的图象记为G,若在图象G上存在点P,使得∠POQ=45°,求n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC沿射线BC向右平移到△DCE的位置,连接AD、BD,则下列结论:①AD=BC;②BD、AC互相平分;③四边形ACED是菱形.其中正确的个数是

A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com