
分析 将二次函数配方成顶点式后确定其顶点坐标及对称轴即可.
解答 解:(1)y=2-2x2的顶点坐标为(0,2),对称轴为x=0;
(2)y=-3(x-1)2+5的顶点坐标为(1,5),对称轴为x=1;
(3)y=4(x+3)2-1的顶点坐标为(-3,-1),对称轴为x=-3;
(4)y=x(5-x)=-(x-2.5)2+6.25的顶点坐标为(2.5,6.25),对称轴为x=2.5;
(5)y=1+2x-x2=-(x-1)2+2的顶点坐标为(1,2),对称轴为x=1;
(6)y=2x2-7x+12=2(x-$\frac{7}{4}$)2+$\frac{47}{8}$的顶点坐标为($\frac{7}{4}$,$\frac{47}{8}$),对称轴为x=$\frac{7}{4}$;.
点评 本题考查了二次函数的性质,能够将二次函数化为顶点式是解答本题的关键,也可以用公式法.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:初中数学 来源: 题型:选择题
| A. | x$>\frac{1}{2}$ | B. | x<-1 | C. | -1<x<$\frac{1}{2}$ | D. | x$>\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
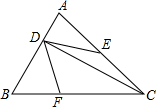 如图,在△ABC中,∠B=60°,CD为AB边上的高,E为AC边的中点,点F在BC边上,∠EDF=60°,若BF=3,CF=5,则AC边的长为2$\sqrt{13}$.
如图,在△ABC中,∠B=60°,CD为AB边上的高,E为AC边的中点,点F在BC边上,∠EDF=60°,若BF=3,CF=5,则AC边的长为2$\sqrt{13}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com