
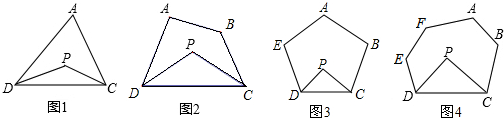
分析 (1)根据角平分线的定义可得∠PDC=$\frac{1}{2}$∠ADC,∠PCD=$\frac{1}{2}$∠ACD,然后根据三角形内角和定理列式整理即可得解;
(2)根据四边形的内角和定理表示出∠ADC+∠BCD,然后同理(1)解答即可;
(3)根据五边形的内角和公式表示出∠EDC+∠BCD,然后同理(1)解答即可;
(4)根据六边形的内角和公式表示出∠EDC+∠BCD,然后同理(1)解答即可;
(5)根据n边形的内角和公式表示出∠EDC+∠BCD,然后同理(1)解答即可.
解答 解:(1)∵DP、CP分别平分∠ADC和∠ACD,
∴∠PDC=$\frac{1}{2}$∠ADC,∠PCD=$\frac{1}{2}$∠ACD,
∴∠DPC=180°-∠PDC-∠PCD
=180°-$\frac{1}{2}$∠ADC-$\frac{1}{2}$∠ACD
=180°-$\frac{1}{2}$(∠ADC+∠ACD)
=180°-$\frac{1}{2}$(180°-∠A)
=90°+$\frac{1}{2}$∠A,
∴如果∠A=60°,那么∠P=120°;如果∠A=90°,那么∠P=135°;如果∠A=x°,则∠P=(90+$\frac{x}{2}$)°;
(2)∵DP、CP分别平分∠ADC和∠BCD,
∴∠PDC=$\frac{1}{2}$∠ADC,∠PCD=$\frac{1}{2}$∠BCD,
∴∠DPC=180°-∠PDC-∠PCD
=180°-$\frac{1}{2}$∠ADC-$\frac{1}{2}$∠BCD
=180°-$\frac{1}{2}$(∠ADC+∠BCD)
=180°-$\frac{1}{2}$(360°-∠A-∠B)
=$\frac{1}{2}$(∠A+∠B);
(3)五边形ABCDEF的内角和为:(5-2)•180°=540°,
∵DP、CP分别平分∠EDC和∠BCD,
∴∠P=$\frac{1}{2}$∠EDC,∠PCD=$\frac{1}{2}$∠BCD,
∴∠P=180°-∠PDC-∠PCD
=180°-$\frac{1}{2}$∠EDC-$\frac{1}{2}$∠BCD
=180°-$\frac{1}{2}$(∠EDC+∠BCD)
=180°-$\frac{1}{2}$(540°-∠A-∠B-∠E)
=$\frac{1}{2}$(∠A+∠B+∠E)-90°,
即∠P=$\frac{1}{2}$(∠A+∠B+∠E)-90°.
(4)六边形ABCDEF的内角和为:(6-2)•180°=720°,
∵DP、CP分别平分∠EDC和∠BCD,
∴∠PDC=$\frac{1}{2}$∠EDC,∠PCD=$\frac{1}{2}$∠BCD,
∴∠P=180°-∠PDC-∠PCD
=180°-$\frac{1}{2}$∠EDC-$\frac{1}{2}$∠BCD
=180°-$\frac{1}{2}$(∠EDC+∠BCD)
=180°-$\frac{1}{2}$(720°-∠A-∠B-∠E-∠F)
=$\frac{1}{2}$(∠A+∠B+∠E+∠F)-180°,
即∠P=$\frac{1}{2}$(∠A+∠B+∠E+∠F)-180°.
(5)同(1)可得,∠P=$\frac{1}{2}$(∠A3+∠A4+∠A5+…∠An)-(n-4)×90°.
故答案为:120,135,(90+$\frac{x}{2}$);$\frac{1}{2}$(∠A+∠B);∠P=$\frac{1}{2}$(∠A+∠B+∠E)-90°;∠P=$\frac{1}{2}$(∠A+∠B+∠E+∠F)-180°;,∠P=$\frac{1}{2}$(∠A3+∠A4+∠A5+…∠An)-(n-4)×90°.
点评 本题考查了三角形的外角性质,三角形的内角和定理,多边形的内角和公式,此类题目根据同一个解答思路求解是解题的关键.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:选择题
| A. | 3到4之间 | B. | 4到5之间 | C. | 5到6之间 | D. | 6到7之间 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
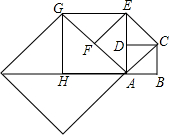 如图,正方形ABCD的边长为1,以对角线AC为边作第二个正方形,再以对角线AE为边作第三个正方形AEGH,如此下去,第n个正方形的边长为($\sqrt{2}$)n-1.
如图,正方形ABCD的边长为1,以对角线AC为边作第二个正方形,再以对角线AE为边作第三个正方形AEGH,如此下去,第n个正方形的边长为($\sqrt{2}$)n-1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com