
【题目】已知:OB、OC、OE是∠AOD内的射线,若∠AOD=130°.
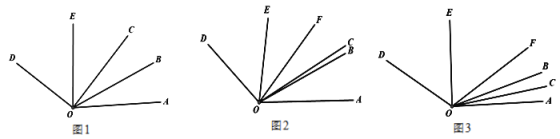
(1)如图1,OB是∠AOC的平分线,OE是∠COD的平分线,∠BOE=_____度;
(2)OF也是∠AOD内的射线,如图2,若∠FOC=20°,OB平分∠AOF,OE平分∠COD,当射线OC绕点O在∠AOF内旋转时,求∠BOE的大小;
(3)在(2)的条件下,当射线OC从边OA开始绕O点以每秒2°的速度逆时针旋转t秒,如图3,若∠AOB:∠DOE=2:3,求t的值.
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案科目:初中数学 来源: 题型:
【题目】2013年1月1日新交通法规开始实施.为了解某社区居民遵守交通法规情况,小明随机选取部分居民就“行人闯红灯现象”进行问卷调查,调查分为“A:从不闯红灯;B:偶尔闯红灯;C:经常闯红灯;D:其他”四种情况,并根据调查结果绘制出部分条形统计图(如图1)和部分扇形统计图(如图2).请根据图中信息,解答下列问题:
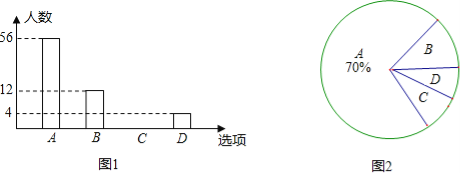
(1)本次调查共选取 名居民;
(2)求出扇形统计图中“C”所对扇形的圆心角的度数,并将条形统计图补充完整;
(3)如果该社区共有居民1600人,估计有多少人从不闯红灯?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】七(1)班的学习小组学习“线段中点”内容时,得到一个很有意思的结论,请跟随他们一起思考.
(1)发现:
如图1,线段![]() ,点
,点![]() 在线段
在线段![]() 上,当点
上,当点![]() 是线段
是线段![]() 和线段
和线段![]() 的中点时,线段
的中点时,线段![]() 的长为_________;若点
的长为_________;若点![]() 在线段
在线段![]() 的延长线上,其他条件不变(请在图2中按题目要求将图补充完整),得到的线段
的延长线上,其他条件不变(请在图2中按题目要求将图补充完整),得到的线段![]() 与线段
与线段![]() 之间的数量关系为_________.
之间的数量关系为_________.
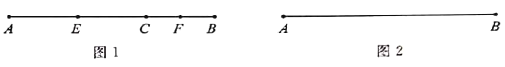
(2)应用:
如图3,现有长为40米的拔河比赛专用绳![]() ,其左右两端各有一段(
,其左右两端各有一段(![]() 和
和![]() )磨损了,磨损后的麻绳不再符合比赛要求. 已知磨损的麻绳总长度不足20米. 小明认为只利用麻绳
)磨损了,磨损后的麻绳不再符合比赛要求. 已知磨损的麻绳总长度不足20米. 小明认为只利用麻绳![]() 和一把剪刀(剪刀只用于剪断麻绳)就可以得到一条长20米的拔河比赛专用绳
和一把剪刀(剪刀只用于剪断麻绳)就可以得到一条长20米的拔河比赛专用绳![]() . 小明所在学习小组认为此法可行,于是他们应用“线段中点”的结论很快做出了符合要求的专用绳
. 小明所在学习小组认为此法可行,于是他们应用“线段中点”的结论很快做出了符合要求的专用绳![]() ,请你尝试着“复原”他们的做法:
,请你尝试着“复原”他们的做法:
①在图中标出点![]() 、点
、点![]() 的位置,并简述画图方法;
的位置,并简述画图方法;
②请说明①题中所标示![]() 点的理由.
点的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数轴上,已知在纸面上有一数轴(如图),折叠纸面.
![]()
(1)若1表示的点与﹣1表示的点重合,则﹣2表示的点与何数表示的点重合;
(2)若﹣1表示的点与5表示的点重合,0表示的点与何数表示的点重合;
(3)若﹣1表示的点与5表示的点之间的线段折叠2次,展开后,请写出所有的折点表示的数?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市场的公平秤如图,把10千克的菜放到秤上,指示盘上的指针转了180°.
(1)如果把2.75千克的菜放在秤上,指针转过多少度?
(2)如果称好0.5千克的菜没有拿走,再把一捆菜放在秤上,指针共转了![]() 那么,后放上的这捆菜有多少千克?
那么,后放上的这捆菜有多少千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,我们定义直线![]() 为抛物线
为抛物线![]() 、b、c为常数,
、b、c为常数,![]() 的“梦想直线”;有一个顶点在抛物线上,另有一个顶点在y轴上的三角形为其“梦想三角形”.
的“梦想直线”;有一个顶点在抛物线上,另有一个顶点在y轴上的三角形为其“梦想三角形”.

已知抛物线![]() 与其“梦想直线”交于A、B两点
与其“梦想直线”交于A、B两点![]() 点A在点B的左侧
点A在点B的左侧![]() ,与x轴负半轴交于点C.
,与x轴负半轴交于点C.
![]() 填空:该抛物线的“梦想直线”的解析式为______,点A的坐标为______,点B的坐标为______;
填空:该抛物线的“梦想直线”的解析式为______,点A的坐标为______,点B的坐标为______;
![]() 如图,点M为线段CB上一动点,将
如图,点M为线段CB上一动点,将![]() 以AM所在直线为对称轴翻折,点C的对称点为N,若
以AM所在直线为对称轴翻折,点C的对称点为N,若![]() 为该抛物线的“梦想三角形”,求点N的坐标;
为该抛物线的“梦想三角形”,求点N的坐标;
![]() 当点E在抛物线的对称轴上运动时,在该抛物线的“梦想直线”上,是否存在点F,使得以点A、C、E、F为顶点的四边形为平行四边形?若存在,请直接写出点E、F的坐标;若不存在,请说明理由.
当点E在抛物线的对称轴上运动时,在该抛物线的“梦想直线”上,是否存在点F,使得以点A、C、E、F为顶点的四边形为平行四边形?若存在,请直接写出点E、F的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某经销商销售一种产品,这种产品的成本价为10元/千克,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于18元/千克,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)之间的函数关系如图所示:
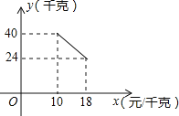
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)求每天的销售利润W(元)与销售价x(元/千克)之间的函数关系式.当销售价为多少时,每天的销售利润最大?最大利润是多少?
(3)该经销商想要每天获得150元的销售利润,销售价应定为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:若一个三位数是312,则百位上数字为3,十位上数字为1,个位上数字为2,这个三位数可表示为3×100+1×10+2;若一个三位数是﹣312,则百位上数字为3,十位上数字为1,个位上数字为2,这个三位数可表示为﹣(3×100+1×10+2);
应用:有一个正的四位数,千位上数字为a,百位上数字为b,十位上数字为c,个位数字为d,且a>d,b﹣c>1.按顺序完成一下运算;
第一步:交换千位和个位上的数字也交换百位和十位上的数字,而构成另一个四位数;
第二步:用原四位数减去第一步构成的四位数,把这个新四位数记为M;
第三步:交换M的百位和十位上的数字,又构成一个新四位数,记为N;
第四部,将M和N相加
(1)第一步构成的另一个四位数可表示为 ;
(2)试判断M百位和十位的数字之和是否为定值?请说明理由.
(3)若M和N相加的值为8892,求a﹣d的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com