
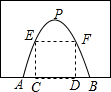
 2015年以来.安徽省高速公路建设稳步推进,相继有十条高速公路建成通车.实现了所有的县在半小时内通达高速.全省高速公路通车里程突破4200公里.如图是某高速单向过山隧道截面设计图.隧道横截面呈抛物线形,设计AB=6米,最高点P点距地面8米.
2015年以来.安徽省高速公路建设稳步推进,相继有十条高速公路建成通车.实现了所有的县在半小时内通达高速.全省高速公路通车里程突破4200公里.如图是某高速单向过山隧道截面设计图.隧道横截面呈抛物线形,设计AB=6米,最高点P点距地面8米.分析 (1)根据题意设抛物线解析式为y=ax2+8,将点B(3,0)代入求得a的值即可得;
(2)令y=3时求得x的值,继而可得隧道的宽度;
(3)令x=2时,求出y的值与4.2比较大小可得.
解答 解:(1)如图,以AB所在直线为横轴.AB的中垂线为纵轴建立平面直角坐标系,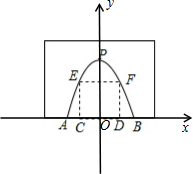
由题意,设抛物线解析式为y=ax2+8,
将点B(3,0)代入,得:9a+8=0,解得:a=-$\frac{8}{9}$,
∴该抛物线的解析式的解析式为:y=-$\frac{8}{9}$x2+8;
(2)当y=3时,-$\frac{8}{9}$x2+8=3,解得:x=±$\frac{3\sqrt{10}}{4}$,
∴隧道的宽度是2×$\frac{3\sqrt{10}}{4}$=$\frac{3\sqrt{10}}{2}$米;
(3)∵当x=2时,y=-$\frac{8}{9}$×22+8=$\frac{40}{9}$>4.2,
∴该隧道设计符合要求.
点评 本题主要考查了二次函数的应用,求抛物线解析式可以使用一般式、顶点式或者交点式,因条件而定.运用二次函数解题时,可以给自变量(或者函数)一个特殊值,求函数(自变量)的值,解答题目的问题.


 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:初中数学 来源: 题型:解答题
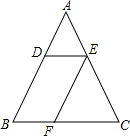 如图,△ABC中,AB=AC,点D在AB上,过点D作BC的平行线,与AC相交于点E,点F在BC上,EF=EC.求证:四边形DBFE是平行四边形.
如图,△ABC中,AB=AC,点D在AB上,过点D作BC的平行线,与AC相交于点E,点F在BC上,EF=EC.求证:四边形DBFE是平行四边形.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
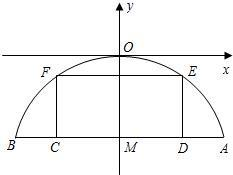 有一座抛物线型拱桥,其水面宽AB为18米,拱顶O离水面AB的距离OM为9米,货船在水面上的部分的横断面是矩形CDEF,如图建立平面直角坐标系.
有一座抛物线型拱桥,其水面宽AB为18米,拱顶O离水面AB的距离OM为9米,货船在水面上的部分的横断面是矩形CDEF,如图建立平面直角坐标系.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com