
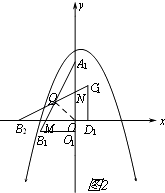
����Ŀ����ֱ������ϵxOy�У�A��0��2����B����1��0��������ABO������ת��ƽ�Ʊ仯��õ���ͼ1��ʾ�ġ�BCD��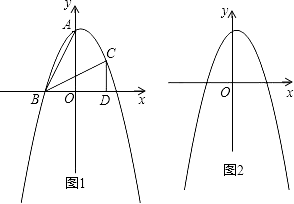
��1����A��B��C����������ߵĽ���ʽ��
��2������AC����P��λ���߶�BC�Ϸ�����������һ���㣬��ֱ��PC����ABC������ֳ�1��3�����֣����ʱ��P�����ꣻ
��3���ֽ���ABO����BCD�ֱ����¡�������1��2���ٶ�ͬʱƽ�ƣ�����ڴ��˶������С�ABO���BCD�ص�������������ֵ��
���𰸡�
��1��
�⣺��A��0��2����B����1��0��������ABO������ת��ƽ�Ʊ仯�õ���BCD��
��BD=OA=2��CD=OB=1����BDC=��AOB=90�㣮
��C��1��1����
�辭��A��B��C����������߽���ʽΪy=ax2+bx+c��
���� 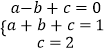 ��
��
�� 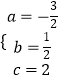
�������߽���ʽΪy=�� ![]() x2+
x2+ ![]() x+2
x+2
��2��
�⣺��ͼ1��ʾ��
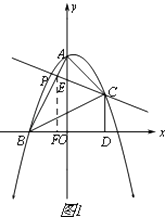
��ֱ��PC��AB���ڵ�E��
��ֱ��PC����ABC������ֳ�1��3�����֣�
�� ![]() =
= ![]() ��
�� ![]() =3��
=3��
��E��EF��OB�ڵ�F����EF��OA��
���BEF�ס�BAO��
�� ![]() ��
��
�൱ ![]() =
= ![]() ʱ��
ʱ�� ![]() ��
��
��EF= ![]() ��BF=
��BF= ![]() ��
��
��E���� ![]() ��
�� ![]() ��
��
��ֱ��PC����ʽΪy=�� ![]() x+
x+ ![]() ��
��
�ੁ ![]() x2+
x2+ ![]() x+2=��
x+2=�� ![]() x+
x+ ![]() ��
��
��x1=�� ![]() ��x2=1����ȥ����
��x2=1����ȥ����
��P���� ![]() ��
�� ![]() ����
����
�� ![]() ʱ��ͬ���ɵã�P����
ʱ��ͬ���ɵã�P���� ![]() ��
�� ![]() ��
��
��3��
�⣺���ABOƽ�Ƶľ���Ϊt����A1B1O1���B2C1D1�ص����ֵ����ΪS��
(i) ��0��t�� ![]() ʱ����A1B1O1���B2C1D1�ص�����Ϊ�ı��Σ�
ʱ����A1B1O1���B2C1D1�ص�����Ϊ�ı��Σ�
��ƽ�Ƶã�A1B1�Ľ���ʽΪy=2x+2��t��A1B1��x�ύ������ΪM�� ![]() ��0����
��0����
C1B2�Ľ���ʽΪy= ![]() x+t+
x+t+ ![]() ��C1B2��y�ύ������ΪN��0��t+
��C1B2��y�ύ������ΪN��0��t+ ![]() ����
����
����ͼ2����C1D1��y���Ҳ�ʱ����0��t�� ![]() ʱ���ص����������ı���ONQM��
ʱ���ص����������ı���ONQM��
��A1B1��x�ύ�ڵ�M��C1B2��y�ύ�ڵ�N��A1B1��C1B2���ڵ�Q������OQ��
�� 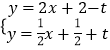 ��
��
�� 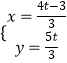 ��
��
��Q�� ![]() ��
�� ![]() ����
����
��S=S��QMO+S��QON
= ![]() ��
�� ![]() ��
�� ![]() +
+ ![]() ����t+
����t+ ![]() ����
���� ![]()
=�� ![]() t2+t+
t2+t+ ![]()
=�� ![]() ��t��
��t�� ![]() ��2+
��2+ ![]() ��
��
��0��t�� ![]() ��
��
�൱t= ![]() ʱ��S�����ֵΪ
ʱ��S�����ֵΪ ![]() ��
��
����ͼ4����C'D'��y����࣬���� ![]() ��t��
��t�� ![]() ʱ����C'�ڡ�A'MO�ڲ������ص��������ı���C'QMD'��
ʱ����C'�ڡ�A'MO�ڲ������ص��������ı���C'QMD'��
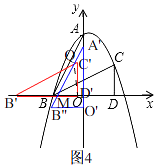
ͬ���ķ����ó���Q�� ![]() ��
�� ![]() ����
����
��S=S��QMD'+S��QON
= ![]() ��[
��[ ![]() ����2t��1��]��
����2t��1��]�� ![]() +
+ ![]() ��1��[
��1��[ ![]() ����2t��1��]
����2t��1��]
=�� ![]() t2+1
t2+1
�� ![]() ��t��
��t�� ![]() ��
��
��S�� ![]() ��
�� ![]()
��ii����ͼ3��ʾ��

�� ![]() ��t��
��t�� ![]() ʱ����A1B1O1���B2C1D1�ص�����Ϊֱ�������Σ�
ʱ����A1B1O1���B2C1D1�ص�����Ϊֱ�������Σ�
��A1B1��x�ύ�ڵ�H��A1B1��C1D1���ڵ�G��
��G��1��2t��4��5t����
��D1H= ![]() +1��2t=
+1��2t= ![]() ��D1G=4��5t��
��D1G=4��5t��
��S= ![]() D1H��D1G=
D1H��D1G= ![]() ��
�� ![]() ����4��5t��=
����4��5t��= ![]() ��5t��4��2��
��5t��4��2��
�൱ ![]() ��t��
��t�� ![]() ʱ��S�����ֵΪ
ʱ��S�����ֵΪ ![]() ��
��
�����������ڴ��˶������С�ABO���BCD�ص�������������ֵΪ ![]() ��
��
����������1������ת��ƽ�Ƶõ�C��1��1�����ô���ϵ������������߽���ʽ����2�����жϳ���BEF�ס�BAO���ٷ�����������м��㣬������Ƚ���������⼴�ɣ���3������ƽ�Ƶõ�A1B1�Ľ���ʽΪy=2x+2��t��A1B1��x�ύ������Ϊ�� ![]() ��0����C1B2�Ľ���ʽΪy=
��0����C1B2�Ľ���ʽΪy= ![]() x+t+
x+t+ ![]() ��C1B2��y�ύ������Ϊ��0��t+
��C1B2��y�ύ������Ϊ��0��t+ ![]() �����ٷ�����������м��㼴�ɣ�
�����ٷ�����������м��㼴�ɣ�


 �����Ļ���������人������ϵ�д�
�����Ļ���������人������ϵ�д� ���������ּ���ÿһ��ȫ�º�����ҵ��ϵ�д�
���������ּ���ÿһ��ȫ�º�����ҵ��ϵ�д� ��ٽ������½������������ϵ�д�
��ٽ������½������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס�����վ���240ǧ�ף��Ӽ�վ����һ���������ٶ�ΪÿСʱ80ǧ�ף�����վ����һ�п쳵���ٶ�ΪÿСʱ120ǧ�ף�
(1)������ͬʱ������������У����ʱ���������540ǧ�ף�
(2)������ͬʱ������ͬ�����(�쳵�ں�)�����ʱ��쳵����������
(3)������ͬʱ������ͬ�����(�����ں�)�����ʱ���������300ǧ�ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=ax2+bx+c��a��0����x�ύ��A��B���㣬��y�ύ�ڵ�C��0��3�����Ҵ������ߵĶ�������ΪM����1��4����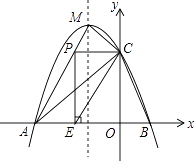
��1����������ߵĽ���ʽ��
��2�����DΪ��֪�����߶Գ����ϵ�����һ�㣬����ACD���ACB������ʱ�����D�����ꣻ
��3����P���߶�AM�ϣ���PC��y�ᴹֱʱ������P��x��Ĵ��ߣ�����ΪE������PCE��ֱ��CE���ۣ�ʹ��P�Ķ�Ӧ��P����P��E��C����ͬһƽ���ڣ��������P�����꣬���жϵ�P���Ƿ��ڸ��������ϣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��DB��AC����DB=![]() AC��E��AC���е㣬
AC��E��AC���е㣬
��1����֤��BC=DE��
��2������AD��BE����Ҫʹ�ı���DBEA�Ǿ��Σ������ABC����ʲô������Ϊʲô��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB��CD��E ��ֱ�� CD �ϵ�һ�㣬�� ��BAE=30�㣬 ��ֱ�� CD �ϵ�һ���㣬M�� AP ���е㣬ֱ�� MN��AP ���� CD ���ڵ� N���� ��BAP=X�㣬��MNE=Y�㣮

��1����ͼ2 �У��� x=12 ʱ����MNE= ����ͼ 3 �У��� x=50 ʱ����MNE= ��
��2���о�������y��x֮���ϵ��ͼ����ͼ4��ʾ�� ������ʱ���ÿ��ĵ��ʾ�����������ͼ��ֱ�ӹ��Ƶ� y=100 ʱ��x= ��

��3��̽������ x= ʱ���� N ��� E �غϣ�
��4��̽������ x>105 ʱ����y��x֮��Ĺ�ϵʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������۲�ͼ�Σ�����������⣺
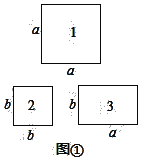
��ͼ����1�ſ�Ƭ�DZ߳�Ϊa�������Σ�2�ſ�Ƭ�DZ߳�Ϊb�������Σ�3�ſ�Ƭ��һ�����Ϳ��ֱ�Ϊa��b�ij����Σ�
��1����ѡȡ1�š�2�š�3�ſ�Ƭ�ֱ�Ϊ1�š�1�š�2�ţ���ƴ��һ�������Σ���ͼ�ڣ����ô�ͼ���͵ij˷���ʽ��______________����������ĸa��b��ʾ��
��2����ѡȡ1�š�2�š�3�ſ�Ƭ�ֱ�Ϊ1�š�2�š�3�ţ���ƴ��һ�������Σ����ص���϶���������ô�ͼ���͵���ʽ�˷�������____________________�����뻭��ͼ�Σ�������ĸa��b��ʾ��
��3�����ͼ�е�a��b��a��b������a2+b2=57��ab=12����a+b��ֵ��
��4����֪��5+2x��2+��3+2x��2=60����5+2x����2x+3����ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������ȤС���������ʵ���о��з��֣����յ����»����ⲿ�����¶ȵı仯���仯����������������ÿ��ҹ�����±仯�����ͬ�����ǽ�һͷ����ǰ����ҹ�����±仯������Ƴ���ͼ�������ͼ��ش����⣺
(1)��һ���У���ʲôʱ�䷶Χ����ͷ���յ������������ģ��������´���������������Ҫ����ʱ�䣿
(2)������12ʱ��ͷ���յ�����Լ�Ƕ��٣�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һЩ������ɵ�ͼ����
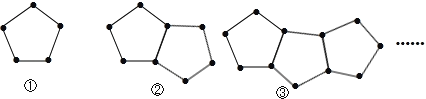
��1���ڵڢٸ�ͼ���� ���������ڵڢڸ�ͼ���� ���������ڵڢ۸�ͼ���� ��������
��2���������ַ�ʽ����ȥ���ڵ�n��ͼ���ö��ٸ�������
��3������һ�°�121������ʱ���ǵڼ���ͼ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
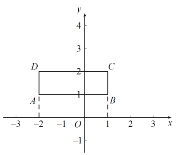
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�������ABCD���ĸ�����ֱ�Ϊ��1��1������1��2������-2��2������-2��1��.�Ըó����μ����ڲ���ÿһ���㶼�������²�������ÿ����ĺ����궼����ͬһ��ʵ��a�������궼����3���ٽ��õ��ĵ�����ƽ��m��m��0������λ������ƽ��2����λ���õ�������ABCD�����ڲ��ĵ㣬���е�A��B��C��D�Ķ�Ӧ��ֱ�ΪA��B��C��D.
��1����A�ĺ�����Ϊ__________���ú�a,m��ʽ�ӱ�ʾ��.
��2����A��������3��1������C��������-3��4����
����a��m��ֵ��
�����Գ�����ABCD�ڲ����������߽磩�ĵ�E(0��y)�������������õ��Ķ�Ӧ��E��Ȼ�ڳ�����ABCD�ڲ����������߽磩����y��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com