
【题目】如图是交警在某个路口统计的某时段来往车辆的车速情况.(单位:千米/时)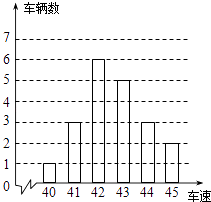
(1)车速的众数是多少?
(2)计算这些车辆的平均数度;
(3)车速的中位数是多少?
【答案】
(1)解:根据条形统计图所给出的数据得:42出现了6次,出现的次数最多,则车速的众数是42千米/时
(2)解:这些车辆的平均数度是:
(40+41×3+42×6+43×5+44×3+45×2)÷20=42.6(千米/时),
答:这些车辆的平均数度是42.6千米/时
(3)解:因为共有20辆车,中位数是第10和11个数的平均数,
所以中位数是42和43的平均数,
(42+43)÷2=42.5(千米/时),
所以车速的中位数是42.5千米/时
【解析】(1)出现的次数最多数据是众数,42出现了6次,易得众数为42千米/小时。
(2)加权平均数的计算注意各个数据的权。
(3)全部数据按从大到小排列,如果是奇数个数则最中间的数为中位数,如果是偶数个数,则最中间的两数的平均数为中位数。所以易得因为共有20辆车,中位数是第10和11个数的平均数所以中位数是42和43的平均数42.5千米/时。
【考点精析】本题主要考查了中位数、众数的相关知识点,需要掌握中位数是唯一的,仅与数据的排列位置有关,它不能充分利用所有数据;众数可能一个,也可能多个,它一定是这组数据中的数才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象交于点
的图象交于点![]() .
.
(1)求这两个函数的表达式;
(2)在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() 为等腰三角形?若存在,求
为等腰三角形?若存在,求![]() 的值,若不存在,说明理由.
的值,若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对任意一个三位数n,如果n满足各个数位上的数字互不相同,且都不为零,那么称这个数为“相异数”,将一个“相异数”任意两个数位上的数字对调后可以得到三个不同的新三位数,把这三个新三位数的和与111的商记为F(n).例如n=123,对调百位与十位上的数字得到213,对调百位与个位上的数字得到321,对调十位与个位上的数字得到132,这三个新三位数的和为213+321+132=666,666÷111=6,所以F(123)=6.
(1)计算:F(243),F(617);
(2)若s,t都是“相异数”,其中s=100x+32,t=150+y(1≤x≤9,1≤y≤9,x,y都是正整数),规定:k=![]() ,当F(s)+F(t)=18时,求k的最大值.
,当F(s)+F(t)=18时,求k的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了丰富学生的校园生活,准备购进一批篮球和足球,其中篮球的单价比足球的单价多40元,用1500元购进的篮球个数与900元购进的足球个数相同,篮球与足球的单价各是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com