
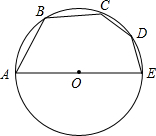
 如图,AE是⊙O的直径,弦AB=BC=4
如图,AE是⊙O的直径,弦AB=BC=4| 2 |
| A、4 | ||
B、4
| ||
C、2
| ||
D、2
|
 |
| AB |
 |
| BC |
 |
| CD |
 |
| DE |
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 5 |
| 2 |
| 5 |
 解:连结BD、OC,作BH⊥CD于H,如图,
解:连结BD、OC,作BH⊥CD于H,如图, |
| AB |
 |
| BC |
 |
| CD |
 |
| DE |
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 2 |
| BH2+DH2 |
| 5 |
| 2 |
| 5 |
| 10 |


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:
| 1 |
| x+1 |
| 1 |
| x+5 |
| 1 |
| x+2 |
| 1 |
| x+4 |
| 6 |
| x2-25 |
| 3 |
| x2+8x+15 |
| 5 |
| x2-2x-15 |
| 1-x |
| x-2 |
| 1 |
| x-2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 石家庄动物园和凤凰山是游客常去的两个景点,动物园(记作A)和凤凰山(记作B)位于笔直的石大高速公路1的同侧,如图所示,要在石大高速公路旁修建一服务区(记作P),向A,B两景点运送游客,并且要使从点P到A,B两地的路程和最短,则此服务区P应建在什么位置?请你用直尺和圆规在如图中画出你的设计方案.(保留作图痕迹,不要求写作法)
石家庄动物园和凤凰山是游客常去的两个景点,动物园(记作A)和凤凰山(记作B)位于笔直的石大高速公路1的同侧,如图所示,要在石大高速公路旁修建一服务区(记作P),向A,B两景点运送游客,并且要使从点P到A,B两地的路程和最短,则此服务区P应建在什么位置?请你用直尺和圆规在如图中画出你的设计方案.(保留作图痕迹,不要求写作法)查看答案和解析>>
科目:初中数学 来源: 题型:
| A、(5,7) |
| B、(2,10) |
| C、(2,10)或(2,4) |
| D、(5,7)或(-1,7) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com