
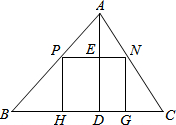
 如图,三角形ABC是一块锐角三角形余料,边BC=12米,高AD=8米,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,这个正方形零件的边长是多少?
如图,三角形ABC是一块锐角三角形余料,边BC=12米,高AD=8米,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,这个正方形零件的边长是多少? 分析 设出边长为x米,由正方形的性质得出,PN∥BC,PH∥AD,根据平行线的性质,可以得出比例关系式,$\frac{PH}{AD}$=$\frac{BP}{AB}$、$\frac{PN}{BC}$=$\frac{AP}{AB}$,代入数据求解即可.
解答  解:设这个正方形零件的边长是x米,
解:设这个正方形零件的边长是x米,
∵矩形为正方形,
∴PN∥BC,PH∥AD,
根据平行线的性质可以得出:$\frac{PH}{AD}$=$\frac{BP}{AB}$、$\frac{PN}{BC}$=$\frac{AP}{AB}$,
由题意知PH=x,AD=8米,BC=12米,PN=x,
即$\frac{x}{8}$=$\frac{BP}{AB}$、$\frac{x}{12}$=$\frac{AP}{AB}$,
∴$\frac{x}{8}$+$\frac{x}{12}$=$\frac{BP}{AB}$+$\frac{AP}{AB}$,
∵AP+BP=AB,
∴$\frac{x}{8}$+$\frac{x}{12}$=1,
解得x=4.8.
答:这个正方形零件的边长是4.8米.
点评 本题考查了正方形以及矩形的性质,结合了平行线的比例关系求解,注意数形结合的运用.


科目:初中数学 来源: 题型:解答题
| 城市 | 伦敦 | 北京 | 东京 | 多伦多 | 纽约 |
| 国际标准时间 | 0 | +8 | +9 | -4 | -5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
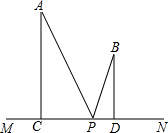 点A,B在直线MN的同侧,A到MN的距离AC=8,B到MN的距离BD=5,已知CD=4,P是直线MN上的一个动点,记PA+PB的最小值为a,|PA-PB|的最大值为b,求a2-b2的值.
点A,B在直线MN的同侧,A到MN的距离AC=8,B到MN的距离BD=5,已知CD=4,P是直线MN上的一个动点,记PA+PB的最小值为a,|PA-PB|的最大值为b,求a2-b2的值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com