
分析 首先观察各点坐标,找出一般规律,然后根据规律确定点A2014的坐标.
解答 解:设An(x,y).
∵当n=1时,A1(1,3),即x=1,y=2×1+1;
当n=2时,A2(2,5),即x=2,y=2×2+1;
当n=3时,A3(3,7),即x=3,y=2×3+1;
当n=4时,A1(4,9),即x=4,y=2×4+1;
…
∴当n=2014时,x=2014,y=2×2014+1,即A2014(2014,4029).
故答案为:(2014,4029).
点评 此题考查点的规律,解决本题的关键在于总结规律.对于寻找规律的题,应通过观察,发现哪些部分没有变化,哪些部分发生了变化,变化的规律是什么.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
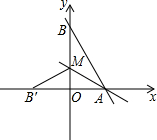 如图,直线y=-$\frac{4}{3}$x+8与x轴,y轴分别交于点A和B,M是OB上的一点,若将△ABM沿AM折叠,点B恰好落在x轴上的点B′处,则△AMO的面积为9.
如图,直线y=-$\frac{4}{3}$x+8与x轴,y轴分别交于点A和B,M是OB上的一点,若将△ABM沿AM折叠,点B恰好落在x轴上的点B′处,则△AMO的面积为9.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,扇形AOB的半径为1,∠AOB=90°,点C在线段OB上移动(不包括端点O、B),以AC为直径作半圆,弧AB与半圆AC围成的阴影部分面积为S1,弧AB与半圆AC及线段BC围成的阴影部分面积为S2,记S=S1+S2.则S的取值范围是0.3925<S<0.5.
如图,扇形AOB的半径为1,∠AOB=90°,点C在线段OB上移动(不包括端点O、B),以AC为直径作半圆,弧AB与半圆AC围成的阴影部分面积为S1,弧AB与半圆AC及线段BC围成的阴影部分面积为S2,记S=S1+S2.则S的取值范围是0.3925<S<0.5.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
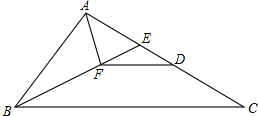 推理填空:完成下列证明:如图,E在△ABC的边AC上,且∠ABF=∠C,AF平分∠BAE交BE于点F,FD∥BC交AC于D.求证:AC-AB=DC.
推理填空:完成下列证明:如图,E在△ABC的边AC上,且∠ABF=∠C,AF平分∠BAE交BE于点F,FD∥BC交AC于D.求证:AC-AB=DC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com