
 小明、小亮、小芳和两个陌生人甲、乙同在如图所示的地下车库等电梯,已知两个陌生人到1至4层的任意一层出电梯.
小明、小亮、小芳和两个陌生人甲、乙同在如图所示的地下车库等电梯,已知两个陌生人到1至4层的任意一层出电梯.分析 (1)列表得出所有等可能的情况数,找出甲乙在同一个楼层的情况数,即可求出所求的概率;
(2)分别求出两人获胜的概率比较得到公平与否,修改规则即可.
解答 解:(1)列表如下:
甲 乙 | 1 | 2 | 3 | 4 |
| 1 | (1,1) | (2,1) | (3,1) | (4,1) |
| 2 | (1,2) | (2,2) | (3,2) | (4,2) |
| 3 | (1,3) | (2,3) | (3,3) | (4,3) |
| 4 | (1,4) | (2,4) | (3,4) | (4,4) |
点评 此题考查了游戏公平性,以及列表法与树状图法,判断游戏公平性就要计算每个事件的概率,概率相等就公平,否则就不公平.


 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
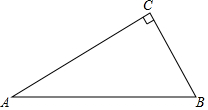 如图,△ABC是直角三角形,∠ACB=90°,∠A=30°
如图,△ABC是直角三角形,∠ACB=90°,∠A=30°查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 在所有连接两点的线中,直线最短 | |
| B. | 延长射线AB | |
| C. | 连接直线外一点和直线上各点的线中,线段最短 | |
| D. | 反向延长线段AB |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com