
分析 (1)因式分解法求解可得;
(2)设$\frac{a}{2}$=$\frac{b}{3}$=k≠0,则a=2k,b=3k,代入求解可得.
解答 解:(1)∵2(x-3)2-(x+3)(x-3)=0,
∴(x-3)(x-9)=0,
则x-3=0或x-9=0,
解得:x=3或x=9;
(2)令$\frac{a}{2}$=$\frac{b}{3}$=k≠0,
则a=2k,b=3k,
∴$\frac{5a-2b}{a+2b}$=$\frac{10k-6k}{2k+6k}$=$\frac{4k}{8k}$=$\frac{1}{2}$.
点评 本题主要考查解一元二次方程的能力和比例的性质,熟练掌握解一元二次方程的几种常用方法:直接开平方法、因式分解法、公式法、配方法,结合方程的特点选择合适、简便的方法和设k法求比例式的值是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,AD平分∠BAC交BC于D,∠MDN的两边分别与AB,AC相交于M,N两点,DM=DN,过D作DF⊥AC于F,证明:AM+AN=2AF.
如图,在△ABC中,AD平分∠BAC交BC于D,∠MDN的两边分别与AB,AC相交于M,N两点,DM=DN,过D作DF⊥AC于F,证明:AM+AN=2AF.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,有下列结论:①CD=ED;②AC+BE=AB;③∠BDE=∠BAC;④DA平分∠CDE;⑤S△ABD:S△ACD=AB:AC.其中,正确的有5个.
如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,有下列结论:①CD=ED;②AC+BE=AB;③∠BDE=∠BAC;④DA平分∠CDE;⑤S△ABD:S△ACD=AB:AC.其中,正确的有5个.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
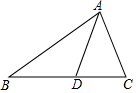 如图,D是△ABC的边BC上任一点,已知AB=4,AD=2,∠DAC=∠B,若△ABD的面积为a,则△ACD的面积为$\frac{1}{3}$a.
如图,D是△ABC的边BC上任一点,已知AB=4,AD=2,∠DAC=∠B,若△ABD的面积为a,则△ACD的面积为$\frac{1}{3}$a.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
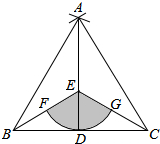 如图,点D是线段BC的中点,分别以点B,C为圆心,BC长为半径画弧,两弧相交于点A,连接AB,AC,AD,点E为AD上一点,连接BE,CE.
如图,点D是线段BC的中点,分别以点B,C为圆心,BC长为半径画弧,两弧相交于点A,连接AB,AC,AD,点E为AD上一点,连接BE,CE. 查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在等腰三角形ABC中,AB=2,∠A=90°,点E为腰AB的中点,点F在底边BC上,且FE⊥CE,则△BEF的面积$\frac{1}{6}$.
如图,在等腰三角形ABC中,AB=2,∠A=90°,点E为腰AB的中点,点F在底边BC上,且FE⊥CE,则△BEF的面积$\frac{1}{6}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com