
分析 (1)根据方程的系数结合根的判别式即可得出关于m的一元一次不等式,解之即可得出结论;
(2)根据根与系数的关系即可得出x1+x2=2(m+1)、x1•x2=m2+2,结合x12+x22=10即可得出关于m的一元二次方程,解之即可得出m的值,再结合(1)的结论即可得出结论.
解答 解:(1)∵方程x2-2(m+1)x+m2+2=0有实数根,
∴△=[-2(m+1)]2-4(m2+2)=8m-4≥0,
解得:m≥$\frac{1}{2}$.
(2)∵方程x2-2(m+1)x+m2+2=0的两实数根分别为x1、x2,
∴x1+x2=2(m+1),x1•x2=m2+2,
∴x12+x22=$({x}_{1}+{x}_{2})^{2}$-2x1•x2=[2(m+1)]2-2(m2+2)=2m2+8m=10,
解得:m1=-5(舍去),m2=1.
∴实数m的值为1.
点评 本题考查了根的判别式、根与系数的关系、解一元一次不等式以及解一元二次方程,解题的关键是:(1)根据方程解的情况找出关于m的一元一次不等式;(2)根据根与系数的关系结合x12+x22=10找出关于m的一元二次方程.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:解答题
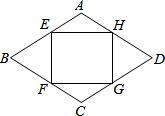 如图,在菱形ABCD的边上依次取点E,F,G,H,使AE=AH=CF=CG,若菱长边长是1,∠A=120°,
如图,在菱形ABCD的边上依次取点E,F,G,H,使AE=AH=CF=CG,若菱长边长是1,∠A=120°,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 开口向下 | B. | 顶点坐标是(1,2) | ||
| C. | 与y轴交点坐标为(0,2) | D. | 与x轴有两个交点 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
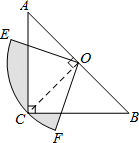 如图,在△ABC中,∠C=90°,AC=BC,斜边AB=4$\sqrt{2}$,O是AB的中点,以O为圆心,线段OC的长为半径画圆心角为90°的扇形OEF,$\widehat{EF}$经过点C,则图中阴影部分的面积为π-2.
如图,在△ABC中,∠C=90°,AC=BC,斜边AB=4$\sqrt{2}$,O是AB的中点,以O为圆心,线段OC的长为半径画圆心角为90°的扇形OEF,$\widehat{EF}$经过点C,则图中阴影部分的面积为π-2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,把矩形ABCD中的AB边向上翻折到AD边上,当点B与点F重合时,折痕与BC边交于点E,连接EF,若四边形EFDC与矩形ABCD恰好相似,若AB=1时,AD的长为( )
如图,把矩形ABCD中的AB边向上翻折到AD边上,当点B与点F重合时,折痕与BC边交于点E,连接EF,若四边形EFDC与矩形ABCD恰好相似,若AB=1时,AD的长为( )| A. | $\frac{1+\sqrt{5}}{2}$ | B. | $\frac{\sqrt{5}-1}{2}$ | C. | 3-$\sqrt{5}$ | D. | $\sqrt{5}$-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直线y=-x+2与过原点的抛物线交于A,B两点,且抛物线的顶点C的坐标为(1,-1).
如图,直线y=-x+2与过原点的抛物线交于A,B两点,且抛物线的顶点C的坐标为(1,-1).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 区县 | 吐鲁番 | 塔城 | 和田 | 伊宁 | 库尔勒 | 阿克苏 | 昌吉 | 呼图壁 | 鄯善 | 哈密 |
| 气温(℃) | 33 | 32 | 32 | 30 | 30 | 29 | 29 | 31 | 30 | 28 |
| A. | 32,32 | B. | 32,30 | C. | 30,30 | D. | 30,32 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com