
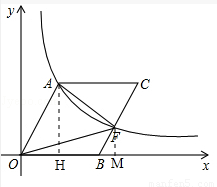
��ͼ�٣�OΪ����ԭ�㣬��B��x����������ϣ��ı���OACB��ƽ���ı��Σ�sin��AOB=������������y=��k��0���ڵ�һ�����ڵ�ͼ����A����BC���ڵ�F��
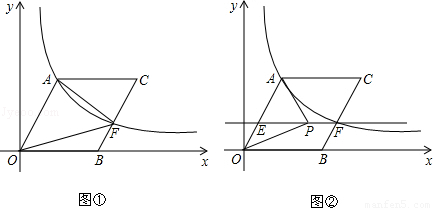
��1����OA=10��������������ʽ��
��2������FΪBC���е㣬�ҡ�AOF�����S=12����OA�ij��͵�C�����ꣻ
��3���ڣ�2���е������£�����F��EF��OB����OA�ڵ�E����ͼ�ڣ�����PΪֱ��EF�ϵ�һ�����㣬����PA��PO���Ƿ���������ĵ�P��ʹ��P��O��AΪ�������������ֱ�������Σ������ڣ���ֱ��д�����е�P�����ꣻ�������ڣ���˵�����ɣ�
��1��y= ��x��0����2��OA=
��x��0����2��OA=
 C��5
C��5 ��
�� ����3��P1��
����3��P1�� ��
�� ����P2����
����P2���� ��
�� ����P3��
����P3��
 ��
�� ����P4����
����P4����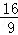
 ��
�� ����
����
����������1������A��AH��OB��H��
��sin��AOB=��OA=10��
��AH=8��OH=6��
��A������Ϊ��6��8������������ã�
8=���ɵã�k=48��
�෴������������ʽ��y= ��x��0����
��x��0����
��2����OA=a��a��0��������F��FM��x����M��
��sin��AOB=��
��AH=a��OH=a��
��S��AOH=?aa=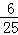 a2��
a2��
��S��AOF=12��
��Sƽ���ı���AOBC=24��
��FΪBC���е㣬
��S��OBF=6��
��BF=a����FBM=��AOB��
��FM=a��BM=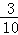 a��
a��
��S��BMF=BM?FM=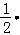 a?
a?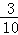 a=
a= a2��
a2��
��S��FOM=S��OBF+S��BMF=6+ a2��
a2��
�ߵ�A��F����y=��ͼ���ϣ�
��S��AOH=k��
�� a2=6+
a2=6+ a2��
a2��
��a=
 ��
��
��OA=
 ��
��
��AH= ��OH=2
��OH=2 ��
��
��Sƽ���ı���AOBC=OB?AH=24��
��OB=AC=3 ��
��
��C��5 ��
�� ����
����
��3���������������
����APO=90��ʱ����OA���������һ��P���ֱ�Ϊ��P1�� ��
�� ����P2����
����P2���� ��
�� ����
����
����PAO=90��ʱ��P3��
 ��
�� ����
����
����POA=90��ʱ��P4����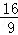
 ��
�� ����
����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
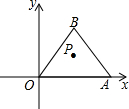 ��ͼ����OΪ����ԭ�㣬��A��2n��0����x�������ᣬ����A�Ƶ�O��ʱ����ת60��õ���B������OAB����P�ǡ�OAB�����ģ�����P������ԭ����ʱ����ת90��õ���P�䣬���P���������
��ͼ����OΪ����ԭ�㣬��A��2n��0����x�������ᣬ����A�Ƶ�O��ʱ����ת60��õ���B������OAB����P�ǡ�OAB�����ģ�����P������ԭ����ʱ����ת90��õ���P�䣬���P����������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
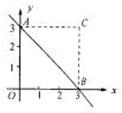 14����ͼ����OΪ����ԭ�㣬OB��OA�ֱ���x�ᡢy���ϣ���A������Ϊ��0��3������B����Ϊ��3��0��������AOB��AB�۵�����O���ڵ�C�������C��������
14����ͼ����OΪ����ԭ�㣬OB��OA�ֱ���x�ᡢy���ϣ���A������Ϊ��0��3������B����Ϊ��3��0��������AOB��AB�۵�����O���ڵ�C�������C���������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ��ʾ��![]() Ϊ����ԭ�㣬һ�κ�����ͼ��
Ϊ����ԭ�㣬һ�κ�����ͼ��![]() �뷴��������
�뷴��������![]() ��ͼ���ڵ�
��ͼ���ڵ�![]()
![]()
![]() �͵�
�͵�![]()
![]() ��
��
��1����![]() ��ֵ�ͷ����������Ľ���ʽ���Ա�����ȡֵ��Χ��
��ֵ�ͷ����������Ľ���ʽ���Ա�����ȡֵ��Χ��
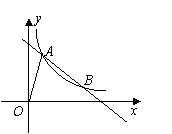
��2������ͼ���жϣ�������ʽ![]() ��
��![]() ����ʱ��x��ȡֵ��Χ��ʲô����3������OB�����OAB�������
����ʱ��x��ȡֵ��Χ��ʲô����3������OB�����OAB�������
 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2008����б�ҵ��ѧ���ԣ����ɹź��ͺ��ؾ�����ѧ���������� ���ͣ������
��ͼ����֪ Ϊ����ԭ�㣬��
Ϊ����ԭ�㣬�� ������Ϊ
������Ϊ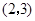 ��
�� �İ뾶Ϊ1����
�İ뾶Ϊ1���� ��ֱ��
��ֱ��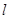 ƽ����
ƽ����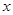 �ᣬ��
�ᣬ��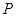 ��
��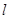 ���˶���
���˶���
��1������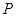 �˶���Բ��ʱ�����߶�
�˶���Բ��ʱ�����߶�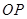 �ij���
�ij���
��2������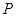 ������Ϊ
������Ϊ ʱ�����ж�ֱ��
ʱ�����ж�ֱ��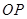 ��
�� ��λ�ù�ϵ����˵�����ɣ�
��λ�ù�ϵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2008����б�ҵ��ѧ���ԣ����ɹź��ͺ��ؾ�����ѧ�������棩 ���ͣ������
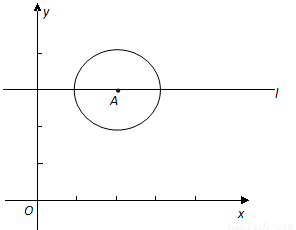
��ͼ����֪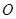 Ϊ����ԭ�㣬��
Ϊ����ԭ�㣬��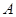 ������Ϊ
������Ϊ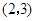 ��
��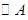 �İ뾶Ϊ1����
�İ뾶Ϊ1����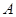 ��ֱ��
��ֱ��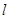 ƽ����
ƽ����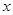 �ᣬ��
�ᣬ��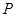 ��
��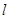 ���˶���
���˶���
��1������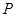 �˶���Բ��ʱ�����߶�
�˶���Բ��ʱ�����߶�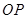 �ij���
�ij���
��2������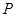 ������Ϊ
������Ϊ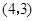 ʱ�����ж�ֱ��
ʱ�����ж�ֱ��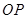 ��
��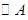 ��λ�ù�ϵ����˵�����ɣ�
��λ�ù�ϵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com