
【题目】如图,四边形![]() 内接于
内接于![]() ,
,![]() ,
,![]() 是对角线。点E在
是对角线。点E在![]() 的延长线上,且
的延长线上,且![]() .
.
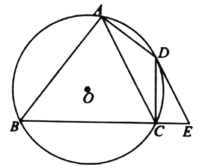
(1)判断![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)![]() 与
与![]() 的延长线交于点F,若
的延长线交于点F,若![]() ,
,![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)DE与![]() 相切,理由见详解;(2)
相切,理由见详解;(2)![]()
【解析】
(1)连接BD,由![]() ,可知BD是直径,根据等量代换和圆周角定理,可得:∠BDC+∠CDE=90°,进而,可得到结论;
,可知BD是直径,根据等量代换和圆周角定理,可得:∠BDC+∠CDE=90°,进而,可得到结论;
(2)设AF=x,易证:FAD~FCB,则![]() ,,推出CF=2x,DF =2x-2,根据勾股定理,列出方程,即可求解.
,,推出CF=2x,DF =2x-2,根据勾股定理,列出方程,即可求解.
(1) 连接BD,
∵![]() ,
,
∴BD是直径,
∴∠BCD=90°,
∴∠DEC+∠CDE=90°,
∵![]() ,
,
∴∠BAC+∠CDE=90°,
∵∠BAC=∠BDC,
∴∠BDC+∠CDE=90°,即:∠BDE=90°,
∴BD⊥DE,
∵点D在![]() 上,
上,
∴DE与![]() 相切.
相切.
(2)设AF=x,
∵![]() ,BD⊥DE,
,BD⊥DE,
∴BD⊥AC,
∴AD=CD=2,AB=CB=4,
∵四边形![]() 内接于
内接于![]() ,
,
∴∠FAD=∠FCB,
∵∠F=∠F,
∴FAD~FCB,
∴![]() ,即:
,即:![]() ,
,
∴CF=2x,
∴DF=CF-CD=2x-2,
∵![]() ,
,
∴∠DAF=90°,
∴![]() ,
,
∴![]() ,解得:
,解得:![]() ,
,![]() (舍去),
(舍去),
∴AF=![]() .
.



科目:初中数学 来源: 题型:
【题目】如图,点O在线段AB上,AO=2,OB=1,OC为射线,且∠BOC=60°,动点P以每秒2个单位长度的速度从点O出发,沿射线OC做匀速运动,设运动时间为t秒.当△ABP是直角三角形时,t的值为( )
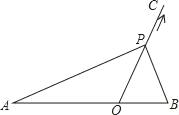
A. ![]() B.
B. ![]() C. 1或
C. 1或![]() D. 1或
D. 1或![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
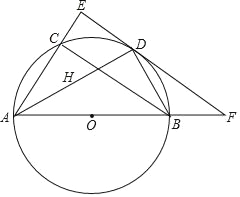
【题目】如图,在直角三角形ABC中,∠ACB=90°,点H是△ABC的内心,AH的延长线和三角形ABC的外接圆O相交于点D,连结DB.
(1)求证:DH=DB;
(2)过点D作BC的平行线交AC、AB的延长线分别于点E、F,已知CE=1,圆O的直径为5.
①求证:EF为圆O的切线;
②求DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究
如图,在平面直角坐标系中,已知抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点(点
两点(点![]() 在点
在点![]() 的右侧),与
的右侧),与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() .
.
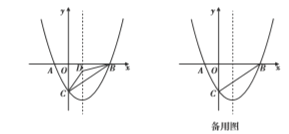
(1)求点![]() 三点的坐标和抛物线的对称轴;
三点的坐标和抛物线的对称轴;
(2)点![]() 为抛物线对称轴上一点,连接
为抛物线对称轴上一点,连接![]() ,
,![]() ,若
,若![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)已知点![]() ,若
,若![]() 是抛物线上一个动点(其中
是抛物线上一个动点(其中![]() ),连接
),连接![]() ,
,![]() ,
,![]() ,求
,求![]() 面积的最大值及此时点
面积的最大值及此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】汽车产业的发展,有效促进我国现代化建设.某汽车销售公司2016年盈利1500万元,到2018年盈利2160万元,且从2016年到2018年,每年盈利的年增长率相同.
(1)求每年盈利的年增长率;
(2)若该公司盈利的年增长率继续保持不变,那么2019年该公司盈利能否达到2500万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
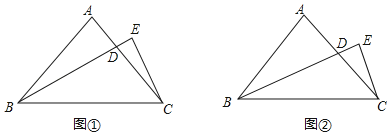
【题目】已知△ABC是等腰直角三角形,∠A=90°,D是腰AC上的一个动点,过点C作CE⊥BD,交BD的延长线于点E,如图①.
(1)求证:ADCD=BDDE;
(2)若BD是边AC的中线,如图②,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() (其中a,b,c为常数)的图象如图所示,有以下结论:①
(其中a,b,c为常数)的图象如图所示,有以下结论:①![]() ;②
;②![]() ;③
;③![]() ;④关于x的一元二次方程
;④关于x的一元二次方程![]() 有两个不相等的实数根.其中正确结论的番号是( )
有两个不相等的实数根.其中正确结论的番号是( )
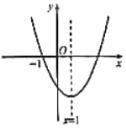
A.①②④B.①③④C.①④D.③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 的正方形网格中,每个小正方形的边长为1,建立如图所示的坐标系.
的正方形网格中,每个小正方形的边长为1,建立如图所示的坐标系.![]() 的三个顶点均在格点上.
的三个顶点均在格点上.
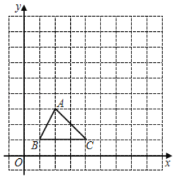
(1)若将![]() 沿x轴对折得到
沿x轴对折得到![]() ,则
,则![]() 的坐标为_______;
的坐标为_______;
(2)以点B为位似中心,将![]() 各边放大为原来的2倍,得到
各边放大为原来的2倍,得到![]() ,请在这个网格中画出
,请在这个网格中画出![]() ;
;
(3)在(2)的条件下,若小明蒙上眼睛在一定距离外,向![]() 的正方形网格内掷小石子,则刚好掷入
的正方形网格内掷小石子,则刚好掷入![]() 的概率是多少?(未掷入图形内则不计次数,重掷一次)
的概率是多少?(未掷入图形内则不计次数,重掷一次)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com