
【题目】如图1,![]() 为等腰三角形,
为等腰三角形,![]() 是底边
是底边![]() 的中点,腰
的中点,腰![]() 与
与![]() 相切于点
相切于点![]() ,底
,底![]() 交
交![]() 于点
于点![]() ,
,![]() .
.
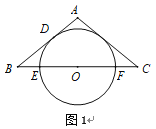
(1)求证:![]() 是
是![]() 的切线;
的切线;
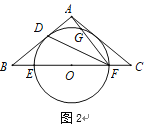
(2)如图2,连接![]() ,
,![]() 交
交![]() 于点
于点![]() ,点
,点![]() 是弧
是弧![]() 的中点,若
的中点,若![]() ,
,![]() ,求
,求![]() 的半径.
的半径.
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:
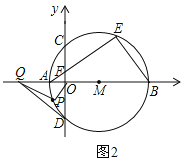
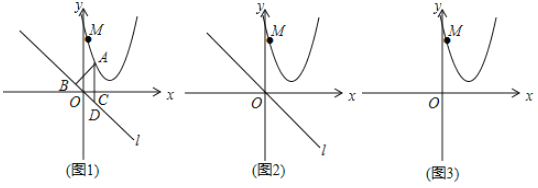
【题目】如图1,在平面直角坐标系内,A,B为x轴上两点,以AB为直径的⊙M交y轴于C,D两点,C为![]() 的中点,弦AE交y轴于点F,且点A的坐标为(﹣2,0),CD=8.
的中点,弦AE交y轴于点F,且点A的坐标为(﹣2,0),CD=8.
(1)求⊙M的半径;
(2)动点P在⊙M的圆周上运动.①如图1,当EP平分∠AEB时,求PN×EP的值;②如图2,过点D作⊙M的切线交x轴于点Q,当点P与点A,B不重合时,![]() 是否为定值?若是,请求出其值;若不是,请说明理由.
是否为定值?若是,请求出其值;若不是,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为备战奥运会,中国女排的姑娘们刻苦训练,为国争光,如图,已知排球场的长度 OD 为 18 米,位于球场中线处球网的高度 AB 为 2.43 米,一队员站在点 O 处发球,排球从点 O 的正上方 1.8 米的 C 点向正前方飞出,当排球运行至离点 O 的水平距离 OE 为 7 米时,到达最高点 G,建立如图所示的平面直角坐标系.
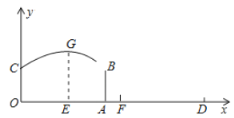
(1)当球上升的最大高度为 3.2 米时,求排球飞行的高度 y(单位:米)与水平距离 x(单位:米)的函数关系式.(不要求写出自变量 x 的取值范围)
(2)在(1)的条件下,对方距球网 0.5 米的点 F 处有一队员,她起跳后的最大高度为 3.1米,问这次她是否可以拦网成功?请通过计算说明.(不考虑排球的大小)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
某同学遇到这样一个问题:在平面直角坐标系![]() 中,已知直线
中,已知直线![]() 点
点![]() 在抛物线
在抛物线![]()
![]() 上,求点
上,求点![]() 到直线
到直线![]() 的距离
的距离![]() .
.
如图1,他过点![]() 作
作![]() 于点
于点![]() 轴分别交
轴分别交![]() 轴于点
轴于点![]() 交直线
交直线![]() 于点
于点![]() .他发现
.他发现![]()
![]() ,可求出
,可求出![]() 的长,再利用
的长,再利用![]() 求出
求出![]() 的长,即为点
的长,即为点![]() 到直线
到直线![]() 的距离
的距离![]() .
.
请回答:
(1)图1中,![]() ,点
,点![]() 到直线
到直线![]() 的距离
的距离![]() .
.
参考该同学思考问题的方法,解决下列问题:
在平面直角坐标系![]() 中,点
中,点![]() 是抛物线
是抛物线![]() 上的一动点,设点
上的一动点,设点![]() 到直线
到直线![]() 的距离为
的距离为![]() .
.
(2)如图2,
①![]() ,则点
,则点![]() 的坐标为 ;
的坐标为 ;
②![]() ,在点
,在点![]() 运动的过程中,求
运动的过程中,求![]() 的最小值;
的最小值;
(3)如图3,![]() ,在点
,在点![]() 运动的过程中,
运动的过程中,![]() 的最小值是 .
的最小值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 、 点
、 点![]() 分别在线段
分别在线段![]() 和线段
和线段![]() 上,
上, ![]() 平分
平分![]() .
.
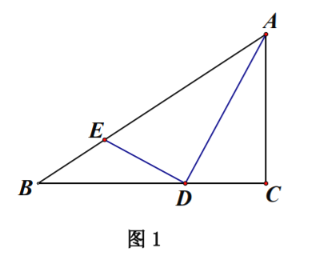
![]() 如图1,求证:
如图1,求证:![]() .
.
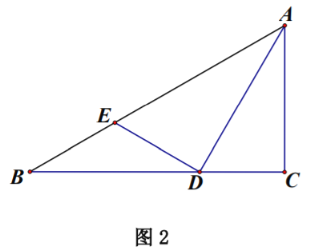
![]() 如图2,若
如图2,若![]() .求证:
.求证:![]() .
.
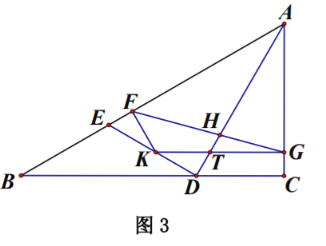
![]() 在
在![]() 问的条件下,如图3, 在线段
问的条件下,如图3, 在线段![]() 上取一点
上取一点![]() ,使
,使![]() .过点
.过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,作
,作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,交
,交![]() 于点
于点![]() ,若
,若![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】使得关于x的分式方程![]() ﹣2=
﹣2=![]() 有正整数解,且关于x的不等式组
有正整数解,且关于x的不等式组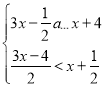 至少有4个整数解,那么符合条件的所有整数a的和为( )
至少有4个整数解,那么符合条件的所有整数a的和为( )
A.﹣20B.﹣17C.﹣9D.﹣5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(﹣1,0)和点B,与y轴交于点C,点C关于抛物线对称轴的对称点为点D,抛物线顶点为H(1,2).
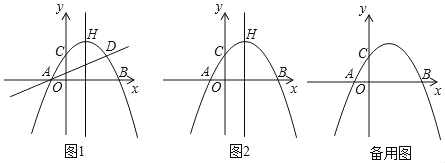
(1)求抛物线的解析式;
(2)点P为直线AD上方抛物线的对称轴上一动点,连接PA,PD.当S△PAD=3,若在x轴上存在一动点Q,使PQ+![]() QB最小,求此时点Q的坐标及PQ+
QB最小,求此时点Q的坐标及PQ+![]() QB的最小值;
QB的最小值;
(3)若点E为抛物线上的动点,点G,F为平面内的点,以BE为边构造以B,E,F,G为顶点的正方形,当顶点F或者G恰好落在y轴上时,求点E的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着“低碳生活,绿色出行”理念的普及,新能源汽车正逐渐成为人们喜爱的交通工具.某汽车销售公司计划购进一批新能源汽车尝试进行销售,据了解2辆A型汽车、3辆B型汽气车的进价共计80万元;3辆A型汽车、2辆B型汽车的进价共计95万元。
(1)求A、B两种型号的汽车每辆进价分别为多少方元?
(2)若该公司计划正好用200万元购进以上两种型号的新能源汽车(两种型号的汽车均购买),请你帮助该公司设计购买方案;
(3)若该汽车销售公司销售1辆A型汽车可获利8000元,销售1辆B型汽车可获利5000元,在(2)中的购买方案中,假如这些新能源汽车全部售出,哪种方案获利最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】第7届世界军人运动会于2019年10月18日在武汉开幕,为备战本届军运会,某运动员进行了多次打靶训练,现随机抽取该运动员部分打靶成绩进行整理分析,共分成四组:![]() (优秀)、
(优秀)、![]() (良好)、
(良好)、![]() (合格)、
(合格)、![]() (不合格),绘制了如下不完整的统计图:
(不合格),绘制了如下不完整的统计图:
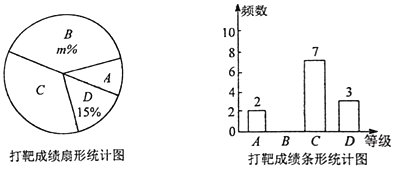
根据以上信息,解答下列问题:
(1)直接写出本次统计成绩的总次数和图中![]() 的值.
的值.
(2)求扇形统计图中![]() (合格)所对应圆心角的度数.
(合格)所对应圆心角的度数.
(3)请补全条形统计图.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com