
【题目】为扶持大学生自主创业,市政府提供了80万元的无息贷款,用于某大学生开办公司,生产并销售自主研发的一种电子产品,并约定用该公司经营的利润逐步偿还无息贷款.已知该电子产品的生产成本为每件40元,公司每月要支付其他费用15万元.该产品每月的销售量y(万件)与销售单价x(元)满足如图所示的一次函数关系:
(1)求每月销售量y(万件)与销售单价x(元)之间的函数关系式.
(2)当销售单价定为多少元时,该公司每月销售利润最大.
(3)若相关部门要求该电子产品的销售单价不得低于其生产成本,且销售每件产品的利润率不能超过25%,则该公司最早用几个月可以还清无息贷款?

【答案】(1) y=-![]() x+8;(2) 60元;(3)6.
x+8;(2) 60元;(3)6.
【解析】
(1)根据题目中所给的图象,确定一次函数图象经过点(60,2)和(70,1),再利用待定系数法求每月销售量y(万件)与销售单价x(元)之间的函数关系式即可;(2)设当销售单价定为x元时,该公司每月销售利润为W万元,根据“总利润=单件的利润×销售量”列出W与x的二次函数关系式,再利用二次函数的性质求解即可;(3)根据题意求得x的取值范围,再求得在这一取值范围内w的最大值,再计算解答即可.
解:(1)设每月销售量y与x的函数解析式为y=kx+b(k≠0),把(60,2)和(70,1)代入得![]() 解得
解得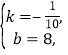 故y=-
故y=-![]() x+8.
x+8.
(2)设当销售单价定为x元时,该公司每月销售利润为W万元,则W=(x-40)![]() -15=-
-15=-![]() x2+12x-335=-
x2+12x-335=-![]() (x-60)2+25,则当销售单价定为60元时,该公司每月销售利润最大.
(x-60)2+25,则当销售单价定为60元时,该公司每月销售利润最大.
(3)由题意得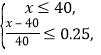 解得40≤x≤50,
解得40≤x≤50,
∵W=-![]() (x-60)2+25,∴抛物线开口向下,当x<60时,W随x的值增大而增大,∴当x=50时,每月有最大利润为W=-
(x-60)2+25,∴抛物线开口向下,当x<60时,W随x的值增大而增大,∴当x=50时,每月有最大利润为W=-![]() ×(50-60)2+25=15(万元),80÷15=
×(50-60)2+25=15(万元),80÷15=![]() =5
=5![]() ,∴该公司最早用6个月可以还清无息贷款.
,∴该公司最早用6个月可以还清无息贷款.


科目:初中数学 来源: 题型:
【题目】如图,为了检验教室里的矩形门框是否合格,某班的四个学习小组用三角板和细绳分别测得如下结果,其中不能判定门框是否合格的是( )
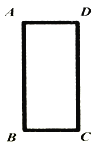
A. AB=CD,AD=BC,AC=BD B. AC=BD,∠B=∠C=90° C. AB=CD,∠B=∠C=90° D. AB=CD,AC=BD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明想利用太阳光测量楼高,他带着皮尺来到一栋楼下,发现对面墙上有这栋楼的影子,针对这种情况,他设计了一种测量方案,具体测量情况如下:如示意图,小明边移动边观察,发现站到点E处时,可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠,且高度恰好相同.此时,测得小明落在墙上的影子高度CD=1.2m,CE=0.8m,CA=30m(点A、E、C在同一直线上).已知小明的身高EF是1.7m,请你帮小明求出楼高AB(结果精确到0.1m).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】菱形AOBC如图放置,A(3,4),先将菱形向左平移9个单位长度,再向下平移1个单位长度,然后沿![]() 轴翻折,最后绕坐标原点O旋转90°得到点C的对应点为点P,则点P的坐标为 ( )
轴翻折,最后绕坐标原点O旋转90°得到点C的对应点为点P,则点P的坐标为 ( )
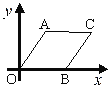
A. (-3,-1) B. (3,1) C. (3,1)(-3,-1) D. (-3,1)(3,-1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,AH⊥BC,垂足为H,且AH=6 cm,点D是AB的中点,点P是AH上一动点,则DP与BP和的最小值是__________cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E是BC的中点,AB⊥BC,DC⊥BC,AE平分∠BAD,下列结论:①∠AED=90°②∠ADE=∠CDE③DE=BE④AD=AB+CD,四个结论中成立的是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD为△ABC外接圆的直径,AD⊥BC,垂足为点F,∠ABC的平分线交AD于点E,连接BD,CD.
(1)求证:BD=CD;
(2)请判断B,E,C三点是否在以D为圆心,以DB为半径的圆上?并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com