
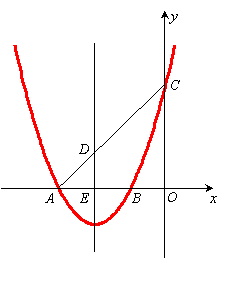
如图12,已知抛物线![]() 交
交![]() 轴于A、B两点,交
轴于A、B两点,交![]() 轴于点C,抛物线的对称轴交
轴于点C,抛物线的对称轴交![]() 轴于点E,点B的坐标为(
轴于点E,点B的坐标为(![]() ,0).
,0).
(1)求抛物线的对称轴及点A的坐标;
(2)在平面直角坐标系![]() 中是否存在点P,与A、B、C三点构成一个平行四边形?若存在,请写出点P的坐标;若不存在,请说明理由;
中是否存在点P,与A、B、C三点构成一个平行四边形?若存在,请写出点P的坐标;若不存在,请说明理由;
(3)连结CA与抛物线的对称轴交于点D,在抛物线上是否存在点M,使得直线CM把四边形DEOC分成面积相等的两部分?若存在,请求出直线CM的解析式;若不存在,请说明理由.
 |
解:(1)① 对称轴![]() ······················· 2分
······················· 2分
② 当![]() 时,有
时,有![]()
解之,得 ![]() ,
,![]()
∴ 点A的坐标为(![]()
![]() ,0).····················· 4分
,0).····················· 4分
(2)满足条件的点P有3个,分别为(![]() ,3),(2,3),(
,3),(2,3),(![]() ,
,![]() ).···· 7分
).···· 7分
(3)存在.······························ 8分
当![]() 时,
时,![]() ∴ 点C的坐标为(0,3)
∴ 点C的坐标为(0,3)
∵ DE∥![]() 轴,AO
轴,AO![]() 3,EO
3,EO![]() 2,AE
2,AE![]() 1,CO
1,CO![]() 3
3
∴ ![]() ∽
∽![]() ∴
∴ ![]() 即
即 ![]() ∴ DE
∴ DE![]() 1····· 9分
1····· 9分
∴ ![]()
![]()
![]() 4
4
在OE上找点F,使OF![]()
![]() ,此时
,此时![]()
![]()
![]() 2,直线CF把四边形DEOC
2,直线CF把四边形DEOC
分成面积相等的两部分,交抛物线于点M.·················· 10分
![]() 设直线CM的解析式为
设直线CM的解析式为![]() ,它经过点
,它经过点![]() .
.
则![]() ···························· 11分
···························· 11分
解之,得 ![]() ∴ 直线CM的解析式为
∴ 直线CM的解析式为 ![]() ·········· 12分
·········· 12分


科目:初中数学 来源: 题型:阅读理解
| |A×m+B×n+C| | ||
|

| 5 |
| 12 |
| 1 |
| 6 |
| 5 |
| 12 |
| 1 |
| 6 |
| |5×1+(-12)×2+(-2)| | ||
|
| 21 |
| 13 |
| 4 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
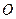 和
和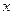 轴上另一点
轴上另一点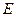 ,顶点
,顶点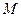 的坐标为
的坐标为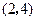 ;矩形
;矩形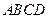 的顶点
的顶点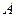 与点
与点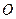 重合,
重合,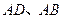 分别在
分别在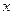 轴、
轴、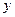 轴上,且
轴上,且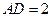 ,
,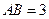 .
.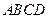 以每秒1个单位长度的速度从图1所示的位置沿
以每秒1个单位长度的速度从图1所示的位置沿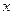 轴的正方向匀速平行移动,同时一动点
轴的正方向匀速平行移动,同时一动点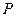 也以相同的速度从点
也以相同的速度从点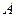 出发向
出发向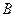 匀速移动.设它们运动的时间为
匀速移动.设它们运动的时间为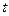 秒(
秒(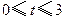 ),直线
),直线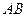 与该抛物线的交点为
与该抛物线的交点为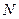 (如图2所示).
(如图2所示).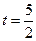 时,判断点
时,判断点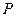 是否在直线
是否在直线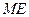 上,并说明理由;
上,并说明理由;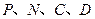 为顶点的多边形面积为
为顶点的多边形面积为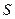 ,试问
,试问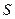 是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.
是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.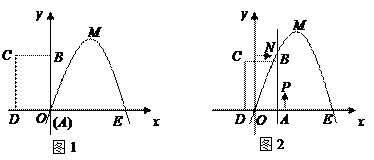
查看答案和解析>>
科目:初中数学 来源:2010年安徽省芜湖市初中毕业学业考试模拟试卷数学卷 题型:解答题
(本小题满分12分)如图1,已知抛物线经过坐标原点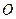 和
和 轴上另一点
轴上另一点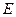 ,顶点
,顶点 的坐标为
的坐标为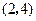 ;矩形
;矩形 的顶点
的顶点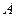 与点
与点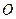 重合,
重合,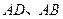 分别在
分别在 轴、
轴、 轴上,且
轴上,且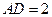 ,
, .
.
(1)求该抛物线所对应的函数关系式;
(2)将矩形 以每秒1个单位长度的速度从图1所示的位置沿
以每秒1个单位长度的速度从图1所示的位置沿 轴的正方向匀速平行移动,同时一动点
轴的正方向匀速平行移动,同时一动点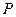 也以相同的速度从点
也以相同的速度从点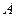 出发向
出发向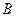 匀速移动.设它们运动的时间为
匀速移动.设它们运动的时间为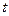 秒(
秒(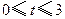 ),直线
),直线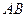 与该抛物线的交点为
与该抛物线的交点为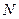 (如图2所示).
(如图2所示).
①当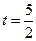 时,判断点
时,判断点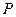 是否在直线
是否在直线 上,并说明理由;
上,并说明理由;
②设以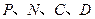 为顶点的多边形面积为
为顶点的多边形面积为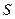 ,试问
,试问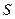 是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.
是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.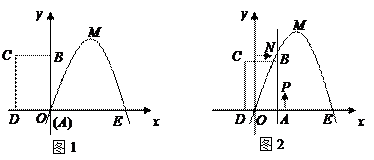
查看答案和解析>>
科目:初中数学 来源: 题型:
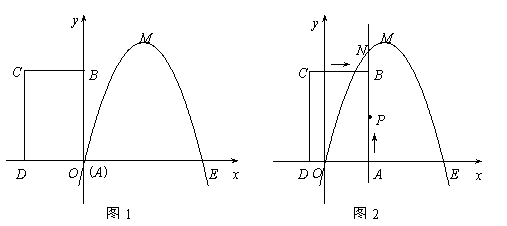
如图1,已知抛物线经过坐标原点O和x轴上另一点E,顶点M的坐标为 (2,4);矩形ABCD的顶点A与点O重合,AD、AB分别在x轴、y轴上,且AD=2,AB=3.
(1)求该抛物线所对应的函数关系式;
(2)将矩形ABCD以每秒1个单位长度的速度从图12所示的位置沿x轴的正方向匀速平行移动,同时一动点P也以相同的速度从点A出发向B匀速移动,设它们运动的时间为t秒(0≤t≤3),直线AB与该抛物线的交点为N(如图2所示).
① 当t=![]() 时,判断点P是否在直线ME上,并说明理由;
时,判断点P是否在直线ME上,并说明理由;
② 设以P、N、C、D为顶点的多边形面积为S,试问S是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com