
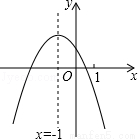
二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:①4ac﹣b2<0;②4a+c<2b;③3b+2c<0;④m(am+b)+b<a(m≠﹣1),其中正确结论的个数是( )
A.4个B.3个C.2个D.1个
B
【解析】
试题分析:∵抛物线和x轴有两个交点,
∴b2﹣4ac>0,
∴4ac﹣b2<0,∴①正确;
∵对称轴是直线x﹣1,和x轴的一个交点在点(0,0)和点(1,0)之间,
∴抛物线和x轴的另一个交点在(﹣3,0)和(﹣2,0)之间,
∴把(﹣2,0)代入抛物线得:y=4a﹣2b+c>0,
∴4a+c>2b,∴②错误;
∵把(1,0)代入抛物线得:y=a+b+c<0,
∴2a+2b+2c<0,
∵b=2a,
∴3b,2c<0,∴③正确;
∵抛物线的对称轴是直线x=﹣1,
∴y=a﹣b+c的值最大,
即把(m,0)(m≠0)代入得:y=am2+bm+c<a﹣b+c,
∴am2+bm+b<a,
即m(am+b)+b<a,∴④正确;
即正确的有3个,
故选B.
考点:二次函数图象与系数的关系


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2014-2015学年内蒙古赤峰市宁城县七年级上学期期末考试数学试卷(解析版) 题型:解答题
(本题满分10分) 2013年6月11日17时18分,神舟十号载人飞船顺利升空,同学们倍受鼓舞,开展了火箭模型的制作比赛,右图为火箭模型的截面图:下面为等腰梯形,中间是长方形,上面是三角形.
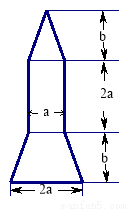
(1)请你用含 的式子表示该截面的面积
的式子表示该截面的面积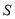 ;
;
(2)当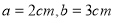 时,求这个火箭模型截面的面积.
时,求这个火箭模型截面的面积.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省新泰市九年级上学期片区竞赛数学试卷(解析版) 题型:选择题
由若干个同样大小的正方体堆积成一个实物,从不同侧面观察到如图所示的投影图,则构成该实物的小正方体个数为( ).
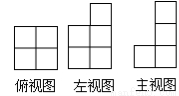
A.6个 B.7个 C.8个 D.9个
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省九年级上学期12月月考数学试卷(解析版) 题型:填空题
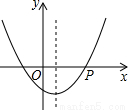
如图,抛物线y=ax2+bx+c(a>0)的对称轴是过点(1,0)且平行于y轴的直线,若点P(4,0)在该抛物线上,则4a﹣2b+c的值为 _________ .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省九年级上学期12月月考数学试卷(解析版) 题型:选择题
二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如下表:
X | ﹣1 | 0 | 1 | 3 |
y | ﹣1 | 3 | 5 | 3 |
下列结论:
(1)ac<0;
(2)当x>1时,y的值随x值的增大而减小.
(3)3是方程ax2+(b﹣1)x+c=0的一个根;
(4)当﹣1<x<3时,ax2+(b﹣1)x+c>0.
其中正确的个数为( )
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省射阳县九年级上学期期末考试数学试卷(解析版) 题型:解答题
(本题满分12分)如图,在平面直角坐标系中,直线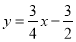 与抛物线
与抛物线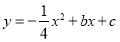 交于A、B两点,点A在x轴上,点B的横坐标为-8.
交于A、B两点,点A在x轴上,点B的横坐标为-8.
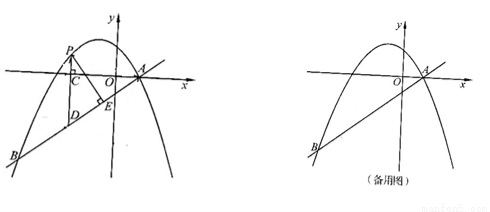
(1)求该抛物线的解析式;
(2)点P是直线AB上方的抛物线上一动点(不与点A、B重合),过点P作x轴的垂线,垂足为C,交直线AB于点D,作PE⊥AB于点E.
①设△PDE的周长为l,点P的横坐标为x,求l关于x的函数关系式,并求出l的最大值;
②连接PA,以PA为边作图示一侧的正方形APFG.随着点P的运动,正方形的大小、位置也随之改变.当顶点F或G恰好落在y轴上时,直接写出对应的点P的坐标.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖南省娄底市九年级上学期期末模拟考试数学试卷(解析版) 题型:解答题
(10分)某商场销售某品牌童装,平均每天可以售出20件,每件盈利40元,为了扩大销售,增加利润,尽量减少库存,经调查发现,每件童装每降价1元,商场平均可多销售2件,若商场每天想盈利1200元,则童装应降价多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com