
【题目】如图,△ABC和△ADE是有公共顶点的等腰直角三角形,∠BAC=∠DAE=90°,点P为射线BD,CE的交点.
(1)求证:BD=CE;
(2)若AB=2,AD=1,把△ADE绕点A旋转,
①当∠EAC=90°时,求PB的长;
②直接写出旋转过程中线段PB长的最小值与最大值.
【答案】
(1)
证明:如图1中,
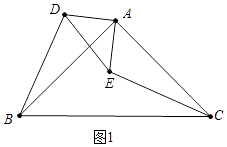
∵△ABC和△ADE是等腰直角三角形,∠BAC=∠DAE=90°,
∴AB=AC,AD=AE,∠DAB=∠CAE,
在△ADB和△AEC中,
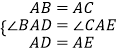
∴△ADB≌△AEC,
∴BD=CE
(2)
解:①a、如图2中,当点E在AB上时,BE=AB﹣AE=1.
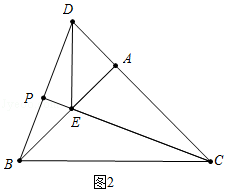
∵∠EAC=90°,
∴CE= ![]() =
= ![]() ,
,
同(1)可证△ADB≌△AEC.
∴∠DBA=∠ECA.
∵∠PEB=∠AEC,
∴△PEB∽△AEC.
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴PB= ![]()
b、如图3中,当点E在BA延长线上时,BE=3.
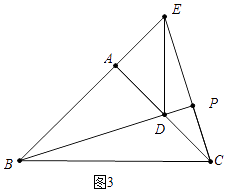
∵∠EAC=90°,
∴CE= ![]() =
= ![]() ,
,
同(1)可证△ADB≌△AEC.
∴∠DBA=∠ECA.
∵∠BEP=∠CEA,
∴△PEB∽△AEC,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴PB= ![]() ,
,
综上,PB= ![]() 或
或 ![]() .②解:a、如图4中,以A为圆心AD为半径画圆,当CE在⊙A下方与⊙A相切时,PB的值最小.
.②解:a、如图4中,以A为圆心AD为半径画圆,当CE在⊙A下方与⊙A相切时,PB的值最小.
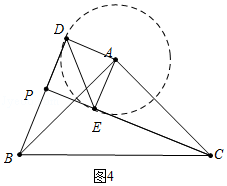
理由:此时∠BCE最小,因此PB最小,(△PBC是直角三角形,斜边BC为定值,∠BCE最小,因此PB最小)
∵AE⊥EC,
∴EC= ![]() =
= ![]() =
= ![]() ,
,
由(1)可知,△ABD≌△ACE,
∴∠ADB=∠AEC=90°,BD=CE= ![]() ,
,
∴∠ADP=∠DAE=∠AEP=90°,
∴四边形AEPD是矩形,
∴PD=AE=1,
∴PB=BD﹣PD= ![]() ﹣1.
﹣1.
b、如图5中,以A为圆心AD为半径画圆,当CE在⊙A上方与⊙A相切时,PB的值最大.
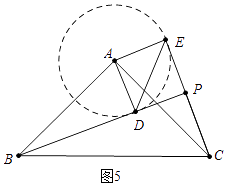
理由:此时∠BCE最大,因此PB最大,(△PBC是直角三角形,斜边BC为定值,∠BCE最大,因此PB最大)
∵AE⊥EC,
∴EC= ![]() =
= ![]() =
= ![]() ,
,
由(1)可知,△ABD≌△ACE,
∴∠ADB=∠AEC=90°,BD=CE= ![]() ,
,
∴∠ADP=∠DAE=∠AEP=90°,
∴四边形AEPD是矩形,
∴PD=AE=1,
∴PB=BD+PD= ![]() +1.
+1.
综上所述,PB长的最小值是 ![]() ﹣1,最大值是
﹣1,最大值是 ![]() +1
+1
【解析】(1)欲证明BD=CE,只要证明△ABD≌△ACE即可.(2)①分两种情形a、如图2中,当点E在AB上时,BE=AB﹣AE=1.由△PEB∽△AEC,得 ![]() =
= ![]() ,由此即可解决问题.b、如图3中,当点E在BA延长线上时,BE=3.解法类似.②a、如图4中,以A为圆心AD为半径画圆,当CE在⊙A下方与⊙A相切时,PB的值最小.b、如图5中,以A为圆心AD为半径画圆,当CE在⊙A上方与⊙A相切时,PB的值最大.分别求出PB即可.
,由此即可解决问题.b、如图3中,当点E在BA延长线上时,BE=3.解法类似.②a、如图4中,以A为圆心AD为半径画圆,当CE在⊙A下方与⊙A相切时,PB的值最小.b、如图5中,以A为圆心AD为半径画圆,当CE在⊙A上方与⊙A相切时,PB的值最大.分别求出PB即可.


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣3x+3与x轴交于点B,与y轴交于点A,以线段AB为边,在第一象限内作正方形ABCD,点C落在双曲线y= ![]() (k≠0)上,将正方形ABCD沿x轴负方向平移a个单位长度,使点D恰好落在双曲线y=
(k≠0)上,将正方形ABCD沿x轴负方向平移a个单位长度,使点D恰好落在双曲线y= ![]() (k≠0)上的点D1处,则a= .
(k≠0)上的点D1处,则a= . 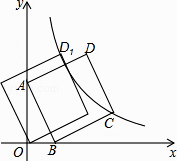
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋子里装着质地、大小都相同的3个红球和2个绿球,随机从中摸出一球,不再放回袋中,充分搅匀后再随机摸出一球.两次都摸到红球的概率是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解九年级学生体育测试情况,以九年级(1)班学生的体育测试成绩为样本,按A,B,C,D四个等级进行统计,并将统计结果绘制成如下的统计图,请你结合图中所给信息解答下列问题: 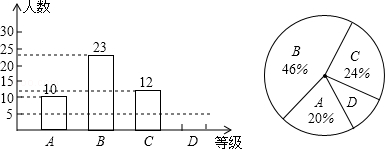
(说明:A级:90分~100分;B级:75分~89分;C级:60分~74分;D级:60分以下)
(1)九年级(1)班体育测试的人数为;
(2)请把条形统计图补充完整;
(3)扇形统计图中A级所在的扇形的圆心角度数是;
(4)若该校九年级有500名学生,请你用此样本估计体育测试中A级和B级的学生人数约为多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线AB:y=![]() x+
x+![]() 分别交x轴、y轴于点B、A两点,C(3,0),D、E分别为线段AO和线段AC上一动点,BE交y轴于点H,且AD=CE.当BD+BE的值最小时,则H点的坐标为( )
分别交x轴、y轴于点B、A两点,C(3,0),D、E分别为线段AO和线段AC上一动点,BE交y轴于点H,且AD=CE.当BD+BE的值最小时,则H点的坐标为( )

A. (0,4) B. (0,5) C. (0,![]() ) D. (0,
) D. (0,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形纸片ABCD中折叠,使顶点B落在边AD的E点上折痕FG交BC于G,交AB于F,若∠AEF=20°,则∠FGB的度数为( ) 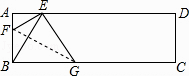
A.25°
B.30°
C.35°
D.40°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一条南北方向的公路上,有一辆出租车停在A地,乘车的第一位客人向南走3千米下车;该车继续向南开,又走了2千米后,上来第二位客人,第二位客人乘车向北走7千米下车,此时恰好有第三位客人上车,先向北走3千米,又调头向南走,结果下车时出租车恰好到了A地.
(1)如果以A地为原点,向北方向为正方向,用1个单位表示1千米,在数轴上表示出第一位客人和第二位客人下车的位置;
(2)第三位客人乘车走了多少千米?
(3)规定出租车的收费标准是4千米内付7元,超过4千米的部分每千米加付1元(不足1千米按1千米算),那么该出租车司机在这三位客人中共收了多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆货车从百货大楼出发负责送货,向东走了 5 千米到达小明家,继续向东走了 1.5 千米到达小红家,然后向西走了 9.5 千米到达小刚家,最后返回百货大楼.
![]()
(1)以百货大楼为原点,向东为正方向,1 个单位长度表示 1 千米,请你在数轴上标出小明、小红、小刚家的位置.(小明家用点 A 表示,小红家用点 B 表示,小刚家用点 C 表示)
(2)小明家与小刚家相距多远?
(3)若货车每千米耗油 0.6 升,那么这辆货车此次送货共耗油多少升?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com