
 如图,在菱形ABCD中,对角线AC=6,BD=8,若过点A作AE⊥BC,垂足为E,则AE的长为$\frac{24}{5}$.
如图,在菱形ABCD中,对角线AC=6,BD=8,若过点A作AE⊥BC,垂足为E,则AE的长为$\frac{24}{5}$. 分析 根据菱形的性质得出BO、CO的长,在RT△BOC中求出BC,利用菱形面积等于对角线乘积的一半,也等于BC×AE,可得出AE的长度.
解答 解:∵四边形ABCD是菱形,
∴CO=$\frac{1}{2}$AC=3,BO=$\frac{1}{2}$BD=4,AO⊥BO,
∴BC=$\sqrt{A{O}^{2}+B{O}^{2}}$=5,
∴S菱形ABCD=$\frac{1}{2}$BD•AC=$\frac{1}{2}$×6×8=24,
∵S菱形ABCD=BC×AE,
∴BC×AE=24,
∴AE=$\frac{24}{5}$.
故答案为:$\frac{24}{5}$.
点评 此题考查了菱形的性质,也涉及了勾股定理,要求我们掌握菱形的面积的两种表示方法,及菱形的对角线互相垂直且平分.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 近几年来,石家庄市区的环境越来越美,随处可见的街心花园成为人们休闲的好去处,现二环路办事处又计划将十字路口附近的小块土地进行绿化改造,他们依地势整理出一块矩形区域ABCD,铺成人们可以活动的砖石地面,又分别以AB、BC、CD、DA为斜边向外做等腰直角三角形(如图所示),通过测量,发现四边形MNGH的周长正好是200米,设AB=x米,BC=y米.
近几年来,石家庄市区的环境越来越美,随处可见的街心花园成为人们休闲的好去处,现二环路办事处又计划将十字路口附近的小块土地进行绿化改造,他们依地势整理出一块矩形区域ABCD,铺成人们可以活动的砖石地面,又分别以AB、BC、CD、DA为斜边向外做等腰直角三角形(如图所示),通过测量,发现四边形MNGH的周长正好是200米,设AB=x米,BC=y米.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
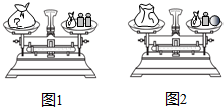 如图1,天平呈平衡状态,其中左侧秤盘中有一袋玻璃球,右侧秤盘中也有一袋玻璃球,还有2个各10克的砝码,将左侧袋中一颗玻璃球移至右侧秤盘,并拿走右侧秤盘的1个砝码后,天平仍呈平衡状态,如图2,现从图2右侧盘中拿掉砝码和袋子外面的玻璃球,只剩下一小袋玻璃球,要使天平保持平衡,则左侧袋中需拿出玻璃球的个数为( )
如图1,天平呈平衡状态,其中左侧秤盘中有一袋玻璃球,右侧秤盘中也有一袋玻璃球,还有2个各10克的砝码,将左侧袋中一颗玻璃球移至右侧秤盘,并拿走右侧秤盘的1个砝码后,天平仍呈平衡状态,如图2,现从图2右侧盘中拿掉砝码和袋子外面的玻璃球,只剩下一小袋玻璃球,要使天平保持平衡,则左侧袋中需拿出玻璃球的个数为( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 已知,在矩形ABCD中,AD=6,AB=8,∠BAD的平分线交DC于点E,∠DAF=22.5°,若点P、Q分别是AD、AF上的动点,则DQ+PQ的最小值为3$\sqrt{2}$.
已知,在矩形ABCD中,AD=6,AB=8,∠BAD的平分线交DC于点E,∠DAF=22.5°,若点P、Q分别是AD、AF上的动点,则DQ+PQ的最小值为3$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示要建一个面积为160平方米的长方形养鸡场,为了节省材料,养鸡场的一边利用原有的一道墙,另三边用铁丝网围成,已知铁丝的长为36米.
如图所示要建一个面积为160平方米的长方形养鸡场,为了节省材料,养鸡场的一边利用原有的一道墙,另三边用铁丝网围成,已知铁丝的长为36米.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com