
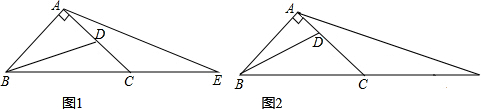
分析 (1)如图1中,作AF⊥BC于F.只要证明△ABD∽△FEA,可得$\frac{AB}{EF}$=$\frac{AD}{AF}$,推出$\frac{AF}{EF}$=$\frac{AD}{AB}$=$\frac{1}{2}$,由此即可解决问题;
(2)结论:BC=CE.证明方法类似(1);
(3)由(1)可知:$\frac{AF}{EF}$=$\frac{AD}{AB}$=$\frac{AD}{AC}$=$\frac{1}{n}$由AF=BF=CF,可得EC=(n-1)AF,由BC=2AF,即可推出$\frac{BC}{EC}$=$\frac{2AF}{(n-1)AF}$=$\frac{2}{n-1}$;
解答 (1)证明:如图1中,作AF⊥BC于F.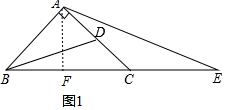
∵AB=AC,∠BAC=90°,AF⊥BC,
∴∠ABC=∠ACB=45°,AF=BF=CF,
∵∠ACB=∠CAE+∠E,∠ABC=∠ABD+∠CBD,∠DBC=∠CAE,
∴∠ABD=∠E,∵∠BAD=∠AFE=90°,
∴△ABD∽△FEA,
∴$\frac{AB}{EF}$=$\frac{AD}{AF}$,
∴$\frac{AF}{EF}$=$\frac{AD}{AB}$=$\frac{1}{2}$,
∴AF=CF=CE=BF,
∴BC=2CE.
(2)结论:BC=CE.
理由:如图2中,作AF⊥BC于F.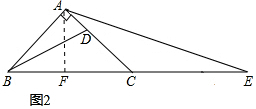
由(1)可知:$\frac{AF}{EF}$=$\frac{AD}{AB}$=$\frac{AD}{AC}$=$\frac{1}{3}$,
∵AF=BF=CF,
∴EC=2AF,
∴BC=CE.
(3)由(1)可知:$\frac{AF}{EF}$=$\frac{AD}{AB}$=$\frac{AD}{AC}$=$\frac{1}{n}$
∵AF=BF=CF,
∴EC=(n-1)AF,
∵BC=2AF,
∴$\frac{BC}{EC}$=$\frac{2AF}{(n-1)AF}$=$\frac{2}{n-1}$,
故答案为$\frac{2}{n-1}$.
点评 本题考查相似三角形综合题,等腰直角三角形的性质等知识,解题的关键是学会添加辅助线,构造相似三角形解决问题,属于中考压轴题.


科目:初中数学 来源:2017届广西马山县民族中学春季学期第一次月考八年级数学试卷(解析版) 题型:单选题
平面直角坐标系上点A、B的坐标分别为(4,0)、(0,3),则线段AB长为( )
A. 6 B. 5 C. 4 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| x | m | 0 | 2 |
| y1 | 4 | 3 | t |
| y2 | 6 | n | -1 |
| A. | -$\frac{1}{3}$ | B. | -3 | C. | $\frac{1}{2}$ | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
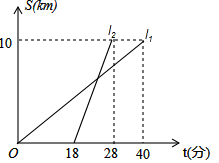 甲、乙两人以相同路线前往距离单位10km的培训中心参加学习,图l1,l2分别表示甲、乙两人前往目的地所走的路程S(千米)随时间t(分)变化的函数图象,以下说法①甲比乙提前12分钟到达;②甲的平均速度为15千米/小时;③甲乙相遇时,乙走了6千米;④乙出发6分钟后追上甲,其中正确的有( )
甲、乙两人以相同路线前往距离单位10km的培训中心参加学习,图l1,l2分别表示甲、乙两人前往目的地所走的路程S(千米)随时间t(分)变化的函数图象,以下说法①甲比乙提前12分钟到达;②甲的平均速度为15千米/小时;③甲乙相遇时,乙走了6千米;④乙出发6分钟后追上甲,其中正确的有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{5}$-$\sqrt{3}$=$\sqrt{2}$ | B. | $\sqrt{\frac{3}{2}}$=$\frac{\sqrt{3}}{2}$ | C. | $\sqrt{12}$=2$\sqrt{3}$ | D. | $\sqrt{(2-\sqrt{5})^{2}}$=2-$\sqrt{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com