
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖ”÷ABCÖŠ£¬”ĻB=90”ć£¬AB=8 cm£¬BC=6 cm£¬P£¬QŹĒ”÷ABC±ßÉĻµÄĮ½øö¶Æµć£¬µćP“ÓµćAæŖŹ¼ŃŲA”śB·½ĻņŌĖ¶Æ£¬ĒŅĖŁ¶ČĪŖ1 cm£¬µćQ“ÓµćBæŖŹ¼ŃŲB”śC·½ĻņŌĖ¶Æ£¬ĒŅĖŁ¶ČĪŖ2 cm/s£¬ĖüĆĒĶ¬Ź±³ö·¢£¬ÉčŌĖ¶ÆµÄŹ±¼äĪŖt s.
£Ø1£©ŌĖ¶Æ¼øĆėŹ±£¬”÷APCŹĒµČŃüČż½ĒŠĪ£æ
£Ø2£©µ±µćQŌŚ±ßCAÉĻŌĖ¶ÆŹ±£¬ĒóÄÜŹ¹”÷BCQ³ÉĪŖµČŃüČż½ĒŠĪµÄŌĖ¶ÆŹ±¼ä.
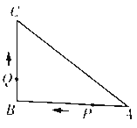
”¾“š°ø”æ£Ø1£©ŌĖ¶Æ![]() sŹ±£¬”÷APCŹĒµČŃüČż½ĒŠĪ.£Ø2£©µ±ŌĖ¶ÆŹ±¼äĪŖ5.5 s »ņ6 s »ņ6.6 sŹ±£¬”÷BCQĪŖµČŃüČż½ĒŠĪ.
sŹ±£¬”÷APCŹĒµČŃüČż½ĒŠĪ.£Ø2£©µ±ŌĖ¶ÆŹ±¼äĪŖ5.5 s »ņ6 s »ņ6.6 sŹ±£¬”÷BCQĪŖµČŃüČż½ĒŠĪ.
”¾½āĪö”æ
£Ø1£©øł¾ŻĢāŅāµĆ£¬AP=PC£¬ĮŠ·½³Ģ£¬Ēó½ā¼“æÉ£»
£Ø2£©·ÖBQ=BC£¬CQ=BCŗĶBQ=CQČżÖÖĒéæö·Ö±šĢÖĀŪµĆµ½¹ŲÓŚtµÄ·½³Ģ£¬Ēó³öt¼“æÉ£®
£Ø1£©ÓÉĢāŅāæÉÖŖAP=t£¬PC=![]()
”ßAP=PC£¬
”ąt=![]() £¬
£¬
½āµĆ£¬t=![]() £¬
£¬
”ą³ö·¢![]() Ćėŗó”÷APCÄÜŠĪ³ÉµČŃüČż½ĒŠĪ£»
Ćėŗó”÷APCÄÜŠĪ³ÉµČŃüČż½ĒŠĪ£»
£Ø2£©ŌŚ”÷ABCÖŠ£¬Óɹ“¹É¶ØĄķæÉĒóµĆAC=10£¬
µ±µćQŌŚACÉĻŹ±£¬AQ=BC+AC-2t=16-2t£¬ĖłŅŌCQ=AC-AQ=10-£Ø16-2t£©=2t-6£¬
µ±BQ=BC=6Ź±£¬ČēĶ¼1£¬¹żB×÷BD”ĶAC£¬ŌņCD=![]() CQ=t-3£¬ŌŚRt”÷ABCÖŠ£¬æÉĒóµĆBD=
CQ=t-3£¬ŌŚRt”÷ABCÖŠ£¬æÉĒóµĆBD=![]() £¬
£¬
ŌŚRt”÷BCDÖŠ£¬Óɹ“¹É¶ØĄķæɵĆBC2=BD2+CD2£¬¼“62=£Ø![]() £©2+£Øt-3£©2£¬
£©2+£Øt-3£©2£¬
½āµĆt=![]() »ņt=-
»ņt=-![]() £¼0£ØÉįČ„£©£»
£¼0£ØÉįČ„£©£»
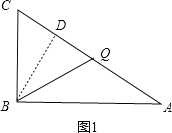
µ±CQ=BC=6Ź±£¬Ōņ2t-6=6£¬½āµĆt=6£¬
µ±CQ=BQŹ±£¬Ōņ”ĻC=”ĻQBC£¬
”ą”ĻC+”ĻA=”ĻCBQ+”ĻQBA£¬
”ą”ĻA=”ĻQBA£¬
”ąQB=QA£¬
”ąCQ=![]() AC=5£¬¼“2t-6=5£¬½āµĆt=5.5£¬
AC=5£¬¼“2t-6=5£¬½āµĆt=5.5£¬
×ŪÉĻæÉÖŖµ±”÷BCQĪŖµČŃüČż½ĒŠĪŹ±£¬t=![]() »ņt=6»ņt=5.5£®
»ņt=6»ņt=5.5£®


 æĘѧŹµŃé»ī¶Æ²įĻµĮŠ“š°ø
æĘѧŹµŃé»ī¶Æ²įĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Å×ĪļĻßy=ax2+bx+c£Øa”Ł0£©ÓėyÖįµÄÕż°ėÖįĻą½»£¬¶„µćŌŚµŚĖÄĻóĻŽ£¬¶Ō³ĘÖįĪŖx=1£¬ĻĀĮŠ½įĀŪ£ŗ¢Łb£¼0£»¢Śa+b£¼0£»¢Ū ![]() £¼©2£»¢Üan2+bn=a£Ø2©n£©2+b£Ø2©n£©£ØnĪŖČĪŅāŹµŹż£©£¬ĘäÖŠÕżČ·µÄ½įĀŪøöŹżŹĒ£Ø £©
£¼©2£»¢Üan2+bn=a£Ø2©n£©2+b£Ø2©n£©£ØnĪŖČĪŅāŹµŹż£©£¬ĘäÖŠÕżČ·µÄ½įĀŪøöŹżŹĒ£Ø £© 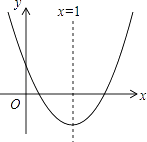
A.1
B.2
C.3
D.4
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
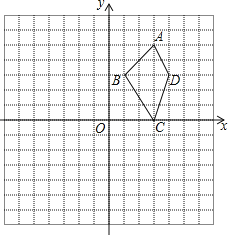
”¾ĢāÄæ”æĖıߊĪABCDŌŚĘ½ĆęÖ±½Ē×ų±źĻµµÄĪ»ÖĆČēĶ¼ĖłŹ¾£¬½«ĖıߊĪABCDĻČĻņĻĀĘ½ŅĘ2øöµ„Ī»£¬ŌŁĻņ×óĘ½ŅĘ3øöµ„Ī»µĆµ½ĖıߊĪA1B1C1D1£¬½ā“šĻĀĮŠø÷Ģā£ŗ
(1)ĒėŌŚĶ¼ÖŠ»³öĖıߊĪA1B1C1D1£»
(2)ĒėŠ“³öĖıߊĪA1B1C1D1µÄ¶„µćB1”¢D1×ų±ź£»
(3)ĒėĒó³öĖıߊĪA1B1C1D1µÄĆ껿£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬A(6£¬a)£¬B(b£¬0)£¬M(0£¬c)£¬PµćĪŖyÖįÉĻŅ»¶Æµć£¬ĒŅ(b©2)2+|a©6|+![]() £½0£®
£½0£®
(1)ĒóµćB”¢MµÄ×ų±ź£»
(2)µ±PµćŌŚĻ߶ĪOMÉĻŌĖ¶ÆŹ±£¬ŹŌĪŹŹĒ·ń“ęŌŚŅ»øöµćPŹ¹S”÷PAB£½13£¬Čō“ęŌŚ£¬ĒėĒó³öPµćµÄ×ų±źÓėABµÄ³¤¶Č£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
(3)²»ĀŪPµćŌĖ¶Æµ½Ö±ĻßOMÉĻµÄČĪŗĪĪ»ÖĆ(²»°üĄØµćO”¢M)£¬”ĻPAM”¢”ĻAPB”¢”ĻPBOČżÕßÖ®¼äŹĒ·ń¶¼“ęŌŚÄ³ÖÖ¹Ģ¶ØµÄŹżĮæ¹ŲĻµ£¬Čē¹ūÓŠ£¬ĒėĄūÓĆĖłŃ§ÖŖŹ¶ÕŅ³ö²¢Ö¤Ć÷£»Čē¹ūƻӊ£¬ĒėĖµĆ÷ĄķÓÉ£®
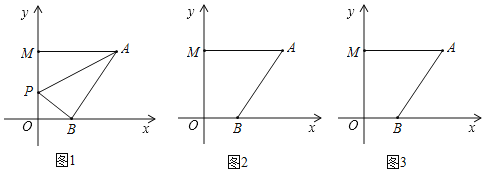
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ÓŠŅ»Ę½ŠŠĖıߊĪABCDÓėŅ»Õż·½ŠĪCEFG£¬ĘäÖŠEµćŌŚADÉĻ£®Čō”ĻECD=35”ć£¬”ĻAEF=15”ć£¬Ōņ”ĻBµÄ¶ČŹżĪŖŗĪ£æ£Ø””””£© 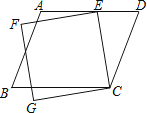
A.50
B.55
C.70
D.75
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ A=3x2+3y2©2xy£¬B=xy©2y2©2x2£®
Ēó£ŗ£Ø1£©2A©3B£®
£Ø2£©Čō|2x©3|=1£¬y2=9£¬|x©y|=y©x£¬Ēó 2A©3B µÄÖµ£®
£Ø3£©Čō x=2£¬y=©4 Ź±£¬“śŹżŹ½ ax3![]() by+5=17£¬ÄĒĆ“µ± x=©4£¬y=©
by+5=17£¬ÄĒĆ“µ± x=©4£¬y=©![]() Ź±£¬Ēó“ś ŹżŹ½ 3ax©24by3+6 µÄÖµ£®
Ź±£¬Ēó“ś ŹżŹ½ 3ax©24by3+6 µÄÖµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅ»øö¼øŗĪĢåÓɼøøö“óŠ”ĻąĶ¬µÄŠ”Į¢·½æé“ī³É£¬“ÓÕżĆęŗĶÉĻĆę¹Ū²ģÕā øö¼øŗĪĢ壬擵½µÄŠĪד¶¼Ņ»Ńł£ØČēĶ¼ĖłŹ¾£©£®
£Ø1£©Õāøö¼øŗĪĢå×īÉŁÓŠ¶ąÉŁøöŠ”Į¢·½æ飬×ī¶ąÓŠ¶ąÉŁøöŠ”Į¢·½æ飻
£Ø2£©µ±°Ś·ÅµÄŠ”Į¢·½æé×ī¶ąŹ±£¬Ēė»³ö“Ó×óĆę¹Ū²ģµ½µÄŹÓĶ¼£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ¶ž“ĪŗÆŹży=x2+bx+cÓėxÖįÖ»ÓŠŅ»øö½»µć£¬ĒŅĶ¼Ļó¹żA£Øx1 £¬ m£©”¢B£Øx1+n£¬m£©Į½µć£¬Ōņm”¢nµÄ¹ŲĻµĪŖ£Ø””””£©
A.m= ![]() n
n
B.m= ![]() n
n
C.m= ![]()
![]()
D.m= ![]()
![]()
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijÉĢµźµŚŅ»“ĪÓĆ600ŌŖ¹ŗ½ų2BĒ¦±ŹČōøÉÖ§£¬µŚ¶ž“ĪÓÖÓĆ600ŌŖ¹ŗ½ųøĆæīĒ¦±Ź£¬µ«Õā“ĪĆæÖ§µÄ½ų¼ŪŹĒµŚŅ»“Ī½ų¼ŪµÄ![]() ±¶£¬¹ŗ½ųŹżĮæ±ČµŚŅ»“ĪÉŁĮĖ30Ö§£®
±¶£¬¹ŗ½ųŹżĮæ±ČµŚŅ»“ĪÉŁĮĖ30Ö§£®
£Ø1£©ĒóµŚŅ»“ĪĆæÖ§Ē¦±ŹµÄ½ų¼ŪŹĒ¶ąÉŁŌŖ£æ
£Ø2£©ČōŅŖĒóÕāĮ½“Ī¹ŗ½ųµÄĒ¦±Ź°“Ķ¬Ņ»¼ŪøńČ«²æĻśŹŪĶź±Ļŗó»ńĄū²»µĶÓŚ420ŌŖ£¬ĪŹĆæÖ§ŹŪ¼ŪÖĮÉŁŹĒ¶ąÉŁŌŖ£æ
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com