
【题目】一个不透明的袋子中装有红、白两种颜色的小球,这些球除颜色外都相同,其中红球有1个,若从中随机摸出一个球,这个球是白球的概率为![]() .
.
(1)求袋子中白球的个数;(请通过列式或列方程解答)
(2)随机摸出一个球后,放回并搅匀,再随机摸出一个球,求两次都摸到相同颜色的小球的概率.(请结合树状图或列表解答)
科目:初中数学 来源: 题型:
【题目】某工厂生产部门为了解本部门工人的生产能力情况,进行了抽样调查.该部门随机抽取了30名工人某天每人加工零件的个数,数据如下:
20 | 21 | 19 | 16 | 27 | 18 | 31 | 29 | 21 | 22 |
25 | 20 | 19 | 22 | 35 | 33 | 19 | 17 | 18 | 29 |
18 | 35 | 22 | 15 | 18 | 18 | 31 | 31 | 19 | 22 |
整理上面数据,得到条形统计图:
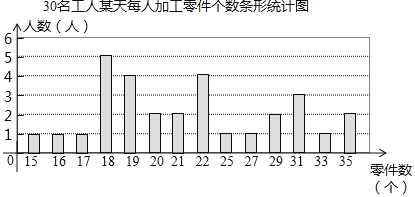
样本数据的平均数、众数、中位数如下表所示:
统计量 | 平均数 | 众数 | 中位数 |
数值 | 23 | m | 21 |
根据以上信息,解答下列问题:
(1)上表中众数m的值为 ;
(2)为调动工人的积极性,该部门根据工人每天加工零件的个数制定了奖励标准,凡达到或超过这个标准的工人将获得奖励.如果想让一半左右的工人能获奖,应根据 来确定奖励标准比较合适.(填“平均数”、“众数”或“中位数”)
(3)该部门规定:每天加工零件的个数达到或超过25个的工人为生产能手.若该部门有300名工人,试估计该部门生产能手的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+1的顶点在直线y=kx+1上,对称轴为直线x=1,有以下四个结论:①ab<0,②b<![]() ,③a=﹣k,④当0<x<1时,ax+b>k,其中正确的结论是( )
,③a=﹣k,④当0<x<1时,ax+b>k,其中正确的结论是( )
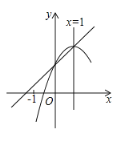
A.①②③B.①③④C.①②④D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E为边CD上一点,将△ADE沿AE折叠至△AD′ E处,AD′ 与CE交于点F,若∠B=55°,∠DAE=20°,则∠FED′ 的大小为( )
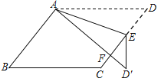
A.20°B.30°
C.35°D.45°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】疫情期间,甲厂欲购买某种无纺布生产口罩,A、B两家无纺布公司各自给出了该种无纺布的销售方案.
A公司方案:无纺布的价格均为每吨1.95万元![]() ;
;
B公司方案:无纺布不超过30吨时,每吨收费2万元;超过30吨时,超过的部分每吨收费1.9万元.
设甲厂在同一公司一次购买无纺布的数量为x吨(x>0).
(Ⅰ)根据题意,填写下表:
一次购买数量(吨) | 10 | 20 | 35 | … |
A公司花费(万元) | 39 | … | ||
B公司花费(万元) | 40 | … |
(Ⅱ) 设在A公司花费![]() 万元,在B公司花费
万元,在B公司花费![]() 万元,分别求
万元,分别求![]() 、
、![]() 关于x的函数解析式;
关于x的函数解析式;
(Ⅲ)如果甲厂所需购买的无纺布是50吨,试通过计算说明选择哪家公司费用较少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图⑴,在△ABC中,∠C=90°,AC=8cm,BC=6cm. 点M由点B出发沿BA方向向点A匀速运动,同时点N由点A出发沿AC方向向点C匀速运动,它们的速度均为2cm/s .连接MN,设运动时间为t(s)﹙0<t<4﹚,解答下列问题:
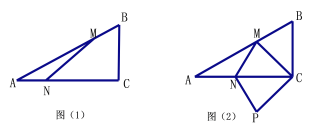
⑴设△AMN的面积为S,求S与t之间的函数关系式,并求出S的最大值;
⑵如图⑵,连接MC,将△MNC沿NC翻折,得到四边形MNPC,当四边形MNPC为菱形时,求t的值;
⑶当t的值为 ,△AMN是等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装公司有![]() 型童装80件,
型童装80件,![]() 型童装120件,分配给下属的“万达”和“万象城”两个专卖店销售,其中140件给万达店,60件给万象城店,且都能卖完,两商店销售这两种童装每件的利润(元)如表:
型童装120件,分配给下属的“万达”和“万象城”两个专卖店销售,其中140件给万达店,60件给万象城店,且都能卖完,两商店销售这两种童装每件的利润(元)如表:
|
| |
万达店 | 100 | 80 |
万象城店 | 80 | 90 |
(1)设分配给万达店![]() 型产品
型产品![]() 件(
件(![]() ),请在下表中用含
),请在下表中用含![]() 的代数式填写:
的代数式填写:
|
| |
万达店 |
| ______ |
万象城店 | ______ | ______ |
若记这家服装公司卖出这200件产品的总利润为![]() (元),求
(元),求![]() 关于
关于![]() 的函数关系.
的函数关系.
(2)现要求总利润不低于18140元,请说明有多少种不同分配方案,并写出各种分配方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在由边长都为1的小正方形组成的网格中,点![]() ,
,![]() ,
,![]() 均为格点,
均为格点,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 中点,
中点,![]() 为
为![]() 上的一个动点.
上的一个动点.
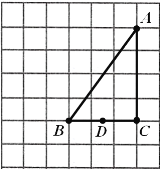
(1)当点![]() 为线段
为线段![]() 中点时,
中点时,![]() 的长度等于__________;
的长度等于__________;
(2)将点![]() 绕点
绕点![]() 逆时针旋转90°得到点
逆时针旋转90°得到点![]() ,连
,连![]() ,当线段
,当线段![]() 取得最小值时,请借助无刻度直尺在给定的网格中画出点
取得最小值时,请借助无刻度直尺在给定的网格中画出点![]() ,点
,点![]() ,并简要说明你是怎么画出点
,并简要说明你是怎么画出点![]() ,点
,点![]() 的:____________________.
的:____________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com