
【题目】在△ABC中,∠BAC=90°,点D是BC上一点,将△ABD沿AD翻折后得到△AED,边AE交BC于点F.


(1)如图①,当AE⊥BC时,写出图中所有与∠B相等的角: ;所有与∠C相等的角: .
(2)若∠C-∠B=50°,∠BAD=x°(0<x≤45) .
① 求∠B的度数;
②是否存在这样的x的值,使得△DEF中有两个角相等.若存在,并求x的值;若不存在,请说明理由.
【答案】(1)∠E、∠CAF;∠CDE、∠BAF; (2)①20°;②30
【解析】
(1)由翻折的性质和平行线的性质即可得与∠B相等的角;由等角代换即可得与∠C相等的角;
(2)①由三角形内角和定理可得![]() ,再由
,再由![]() 根据角的和差计算即可得∠C的度数,进而得∠B的度数.
根据角的和差计算即可得∠C的度数,进而得∠B的度数.
②根据翻折的性质和三角形外角及三角形内角和定理,用含x的代数式表示出∠FDE、∠DFE的度数,分三种情况讨论求出符合题意的x值即可.
(1)由翻折的性质可得:∠E=∠B,
∵∠BAC=90°,AE⊥BC,
∴∠DFE=90°,
∴180°-∠BAC=180°-∠DFE=90°,
即:∠B+∠C=∠E+∠FDE=90°,
∴∠C=∠FDE,
∴AC∥DE,
∴∠CAF=∠E,
∴∠CAF=∠E=∠B
故与∠B相等的角有∠CAF和∠E;
∵∠BAC=90°,AE⊥BC,
∴∠BAF+∠CAF=90°, ∠CFA=180°-(∠CAF+∠C)=90°
∴∠BAF+∠CAF=∠CAF+∠C=90°
∴∠BAF=∠C
又AC∥DE,
∴∠C=∠CDE,
∴故与∠C相等的角有∠CDE、∠BAF;
(2)①∵![]()
∴![]()
又∵![]() ,
,
∴∠C=70°,∠B=20°;
②∵∠BAD=x°, ∠B=20°则![]() ,
,![]() ,
,
由翻折可知:∵![]() ,
, ![]() ,
,
∴![]() ,
, ![]() ,
,
当∠FDE=∠DFE时,![]() , 解得:
, 解得:![]() ;
;
当∠FDE=∠E时,![]() ,解得:
,解得:![]() (因为0<x≤45,故舍去);
(因为0<x≤45,故舍去);
当∠DFE=∠E时,![]() ,解得:
,解得:![]() (因为0<x≤45,故舍去);
(因为0<x≤45,故舍去);
综上所述,存在这样的x的值,使得△DEF中有两个角相等.且![]() .
.


科目:初中数学 来源: 题型:
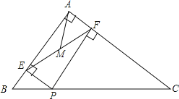
【题目】Rt△ABC中,∠BAC=90°,AB=3,AC=4,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图甲,AB∥CD,试问∠2与∠1+∠3的关系是什么,为什么?
(2)如图乙,AB∥CD,试问∠2+∠4与∠1+∠3+∠5一样大吗?为什么?
(3)如图丙,AB∥CD,试问∠2+∠4+∠6与∠1+∠3+∠5+∠7哪个大?为什么?
你能将它们推广到一般情况吗?请写出你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在10×10的正方形网格中,每个小正方形的边长为1个单位长度.△ABC的顶点都在正方形网格的格点上,且通过两次平移(沿网格线方向作上下或左右平移)后得到△A'B'C',点C的对应点是直线上的格点C'.
(1)画出△A'B'C';
(2)在BC上找一点P,使AP平分△ABC的面积;
(3)试在直线l上画出所有的格点Q,使得由点A'、B'、C'、Q四点围成的四边形的面积为9.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c交x轴于A、B两点,交y轴于点C,已知抛物线的对称轴为x=1,B(3,0),C(0,﹣3),
(1)求二次函数y=ax2+bx+c的解析式;
(2)在抛物线对称轴上是否存在一点P,使点P到B、C两点距离之差最大?若存在,求出P点坐标;若不存在,请说明理由;
(3)平行于x轴的一条直线交抛物线于M、N两点,若以MN为直径的圆恰好与x轴相切,求此圆的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四张编号为A,B,C,D的卡片(除编号外,其余完全相同)的正面分别写上如图所示的正整数后,背面向上,洗匀放好.
(1)我们知道,满足a2+b2=c2的三个正整数a,b,c成为勾股数,嘉嘉从中随机抽取一张,求抽到的卡片上的数是勾股数的概率P1;
(2)琪琪从中随机抽取一张(不放回),再从剩下的卡片中随机抽取一张(卡片用A,B,C,D表示).请用列表或画树形图的方法求抽到的两张卡片上的数都是勾股数的概率P2 , 并指出她与嘉嘉抽到勾股数的可能性一样吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】D,E分别是不等边三角形ABC(即AB≠BC≠AC)的边AB,AC的中点.O是△ABC所在平面上的动点,连接OB,OC,点G,F分别是OB,OC的中点,顺次连接点D,G,F,E.
(1)如图,当点O在△ABC的内部时,求证:四边形DGFE是平行四边形;
(2)若四边形DGFE是菱形,则OA与BC应满足怎样的数量关系?(直接写出答案,不需要说明理由.)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com