
 已知:a是-1,且a、b、c满足(c-6)2+|2a+b|=0,请回答问题:
已知:a是-1,且a、b、c满足(c-6)2+|2a+b|=0,请回答问题:分析 (1)根据非负数的性质可得;
(2)(a)根据两点间距离公式列出算式,化简可得;
(b)分别根据-1≤x<2、2≤x<6、x≥6结合绝对值性质,去绝对值符号后化简可得.
解答 解:(1)∵(c-6)2+|2a+b|=0,
∴c=6,2a+b=0,即b=-2a,
又∵a=-1,
∴b=2,
故答案为:2,6;
(2)(a)∵PA=x-(-1)=x+1,PB=2-x,PC=6-x,
∴PA+PB+PC=x+1+2-x+6-x=9-x;|x+1|-|x-2|+2|x-6|;
(b)当-1≤x<2时,原式=x+1+x-2-2(x-6)=11;
当2≤x<6时,原式=x+1-(x-2)-2(x-6)=-2x+15;
当x≥6时,原式=x+1-(x-2)+2(x-6)=2x-9.
点评 本题主要考查非负数的性质、两点间距离公式、绝对值的性质及整式的化简,根据点P的位置分类讨论是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
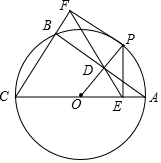 如图,⊙O是△ABC的外接圆,AC是直径,过点O作OD⊥AB于点D,延长DO交⊙O于点P,过点P作PE⊥AC于点E,作射线ED交CB的延长线于F点,连接PF.
如图,⊙O是△ABC的外接圆,AC是直径,过点O作OD⊥AB于点D,延长DO交⊙O于点P,过点P作PE⊥AC于点E,作射线ED交CB的延长线于F点,连接PF.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
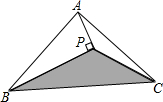 如图,△PBC的面积为10cm2,AP垂直∠B的平分线BP于P,则△ABC的面积为( )
如图,△PBC的面积为10cm2,AP垂直∠B的平分线BP于P,则△ABC的面积为( )| A. | 10cm2 | B. | 12cm2 | C. | 16cm2 | D. | 20cm2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
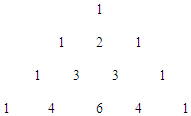 我们已经知道:
我们已经知道:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
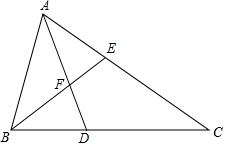 如图,在△ABC中,AD平分∠BAC,BE平分∠ABC,AD、BE相交于点F,且AB+BD=AC.
如图,在△ABC中,AD平分∠BAC,BE平分∠ABC,AD、BE相交于点F,且AB+BD=AC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com