
如图,点B1是抛物线 的顶点,点A1、A2都在该抛物线上,四边形OA1B1C1、OA2B2C2均为正方形,点B2在y轴上,直线C2B2与该抛物线交于点
的顶点,点A1、A2都在该抛物线上,四边形OA1B1C1、OA2B2C2均为正方形,点B2在y轴上,直线C2B2与该抛物线交于点 ,则
,则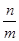 的值是 .
的值是 . 
 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
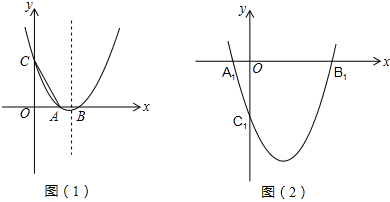
 如图,点A在x轴的负半轴上,OA=4,AB=OB=
如图,点A在x轴的负半轴上,OA=4,AB=OB=| 5 |
| 9 |
| 2 |
| 9 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
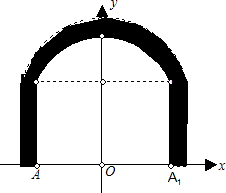 如图所示,是一条高速公路的隧道口在平面直角坐标系上的示意图,点A 和A1、点B和B1分别关于y轴对称,隧道拱部分BCB1为一条抛物线,最高点C离路面AA1的距离为8米,点B离路面为6米,隧道的宽度AA1为16米;则隧道拱抛物线BCB1的函数解析式
如图所示,是一条高速公路的隧道口在平面直角坐标系上的示意图,点A 和A1、点B和B1分别关于y轴对称,隧道拱部分BCB1为一条抛物线,最高点C离路面AA1的距离为8米,点B离路面为6米,隧道的宽度AA1为16米;则隧道拱抛物线BCB1的函数解析式查看答案和解析>>
科目:初中数学 来源:2012-2013学年广西贵港市毕业班第四次教学质量监测试卷数学试卷(解析版) 题型:填空题
如图,点B1是抛物线 的顶点,点A1、A2都在该抛物线上,四边形OA1B1C1、OA2B2C2均为正方形,点B2在y轴上,直线C2B2与该抛物线交于点
的顶点,点A1、A2都在该抛物线上,四边形OA1B1C1、OA2B2C2均为正方形,点B2在y轴上,直线C2B2与该抛物线交于点 ,则
,则 的值是 .
的值是 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com