
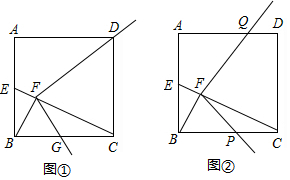
分析 (1)先根据勾股定理求得CE的长,再根据$\frac{BE}{CE}$=$\frac{EF}{EB}$,∠FEB=∠BEC,判定△BEF∽△CEB即可;
(2)先过F作MN⊥BC于N,交AD于M,作FH⊥AB于H,根据平行线分线段成比例定理,求得DM、FM、FN的长,再根据△DMF∽△FNG,求得NG的长,最后根据勾股定理即可求得FG的长;
(3)分两种情况讨论:当0<x<5时,当5<x<8时,分别根据△QMF∽△FNP,求得NP=$\frac{24}{8-x}$,进而得到CP的长,最后计算△FCP的面积,即可得到y与x的函数解析式.而当8≤x<10时,射线FG与BC无交点,故此时△CFP不存在.
解答 解:(1)∵四边形ABCD为正方形,边长为10,点E为AB的中点,
∴EB=5,BC=10,
∴Rt△BCE中,CE=$\sqrt{{5}^{2}+1{0}^{2}}$=5$\sqrt{5}$,
∴$\frac{BE}{CE}$=$\frac{5}{5\sqrt{5}}$=$\frac{\sqrt{5}}{5}$,
又∵$\frac{EF}{FC}$=$\frac{1}{4}$,
∴EF=$\sqrt{5}$,
∴$\frac{EF}{EB}$=$\frac{\sqrt{5}}{5}$,
∴$\frac{BE}{CE}$=$\frac{EF}{EB}$,
又∵∠FEB=∠BEC,
∴△BEF∽△CEB;
(2)如图①,过F作MN⊥BC于N,交AD于M,作FH⊥AB于H,则NM⊥AD,
∵HF∥BC,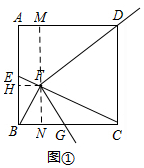
∴$\frac{EH}{HB}$=$\frac{EF}{FC}$=$\frac{1}{4}$,
∴EH=1,HB=4=FN,
∴AH=MF=6,
∵FN∥AB,
∴$\frac{BN}{NC}$=$\frac{EF}{FC}$=$\frac{1}{4}$,
∴NB=2,NC=8=DM,
∵∠DFG=90°,∠DMF=90°,
∴∠MDF+∠MFD=90°=∠NFG+∠MFD,
∴∠MDF=∠NFG,
又∵∠DMF=∠FNG=90°,
∴△DMF∽△FNG,
∴$\frac{NG}{MF}$=$\frac{FN}{DM}$,
即$\frac{NG}{6}$=$\frac{4}{8}$,
解得NG=3,
∴Rt△FGN中,FG=$\sqrt{{3}^{2}+{4}^{2}}$=5;
(3)如图②所示,当0<x<5时,MQ=8-x,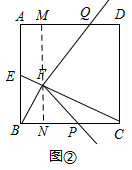
由(2)可得△QMF∽△FNP,
∴$\frac{NP}{MF}$=$\frac{NF}{MQ}$,
即$\frac{NP}{6}$=$\frac{4}{8-x}$,
解得NP=$\frac{24}{8-x}$,
∴CP=CN-NP=8-$\frac{24}{8-x}$,
∴△FCP的面积=$\frac{1}{2}$×CP×FN,
即y=$\frac{1}{2}$×(8-$\frac{24}{8-x}$)×4,
∴y=16-$\frac{48}{8-x}$(0<x<5);
如图③所示,当5<x<8时,MQ=8-x,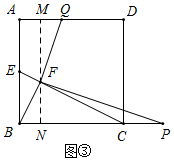
由(2)可得△QMF∽△FNP,
∴$\frac{NP}{MF}$=$\frac{NF}{MQ}$,
即$\frac{NP}{6}$=$\frac{4}{8-x}$,
解得NP=$\frac{24}{8-x}$,
∴CP=NP-CN=$\frac{24}{8-x}$-8,
∴△FCP的面积=$\frac{1}{2}$×CP×FN,
即y=$\frac{1}{2}$×($\frac{24}{8-x}$-8)×4,
∴y=$\frac{48}{8-x}$-16(5<x<8);
当8≤x<10时,射线FG与BC无交点,故此时△CFP不存在.
综上所述,y与x的函数解析式为:y=$\left\{\begin{array}{l}{16-\frac{48}{8-x}(0<x<5)}\\{\frac{48}{8-x}-16(5<x<8)}\end{array}\right.$.
点评 本题是相似三角形综合题,主要考查了相似三角形的判定与性质,勾股定理以及平行线分线段成比例定理的综合应用,解决问题的关键是作辅助线构造矩形和相似三角形.解题时注意分类思想的运用.


 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:初中数学 来源: 题型:解答题
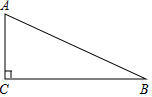 已知△ABC中,∠C=90°,AC=8cm,AB=17cm.
已知△ABC中,∠C=90°,AC=8cm,AB=17cm.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
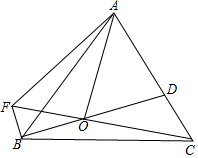 如图,点O为等边△ABC内一点,OA=2$\sqrt{5}$,OC=$\sqrt{15}$,连接BO并延长交AC于点D.若∠DOC=30°,过点B作BF⊥BD交CO延长线于点F,连接AF,则AF=$\frac{4\sqrt{15}}{3}$.
如图,点O为等边△ABC内一点,OA=2$\sqrt{5}$,OC=$\sqrt{15}$,连接BO并延长交AC于点D.若∠DOC=30°,过点B作BF⊥BD交CO延长线于点F,连接AF,则AF=$\frac{4\sqrt{15}}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
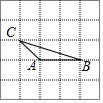 如图,由25个同样大小的小正方形组成的正方形网格中,△ABC是格点三角形(每个顶点都是格点),在这个正方形网格中画另一个格点三角形,使得它与△ABC全等且仅有一条公共边,则符合要求的三角形共能画( )
如图,由25个同样大小的小正方形组成的正方形网格中,△ABC是格点三角形(每个顶点都是格点),在这个正方形网格中画另一个格点三角形,使得它与△ABC全等且仅有一条公共边,则符合要求的三角形共能画( )| A. | 5个 | B. | 6个 | C. | 7个 | D. | 8个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
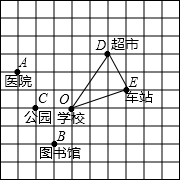 如图,10×10的正方形网格(每个小正方形的边长为1)表示某市部分简图,学校,医院、图书馆、公园、超市、车站的位置分别用点O、A、B、C、D、E表示,请你完成下列问题:
如图,10×10的正方形网格(每个小正方形的边长为1)表示某市部分简图,学校,医院、图书馆、公园、超市、车站的位置分别用点O、A、B、C、D、E表示,请你完成下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x1=1.6,x2=0.6 | B. | x1=-1.6,x2=0.6 | C. | x1=1.6,x2=-0.6 | D. | x1=-1.6,x2=-0.6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=2x+3 | B. | y=2x-3 | C. | y=-2x+3 | D. | y=-2x-3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com