
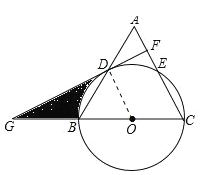
【题目】在等腰△ABC中,AC=BC,以BC为直径的⊙O分别与AB,AC相交于点D,E,过点D作DF⊥AC,垂足为点F.
(1)求证:DF是⊙O的切线;
(2)分别延长CB,FD,相交于点G,∠A=60°,⊙O的半径为6,求阴影部分的面积.

【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)连接OD,由等腰三角形的性质证出∠A=∠ODB,得出OD∥AC,证出DF⊥OD,即可得出结论;
(2)证明△OBD是等边三角形,由等边三角形的性质得出∠BOD=60°,求出∠G=30°,由直角三角形的性质得出OG=2OD=2×6=12,由勾股定理得出DG的长,阴影部分的面积=△ODG的面积﹣扇形OBD的面积,即可得出答案.
试题解析:(1)证明:连接OD,如图所示:
∵AC=BC,OB=OD,∴∠ABC=∠A,∠ABC=∠ODB,∴∠A=∠ODB,∴OD∥AC,∵DF⊥AC,∴DF⊥OD,∵OD是⊙O的半径,∴DF是⊙O的切线;
(2)解:∵AC=BC,∠A=60°,∴△ABC是等边三角形,∴ABC=60°,∵OD=OB,∴△OBD是等边三角形,∴∠BOD=60°,∵DF⊥OD,∴∠ODG=90°,∴∠G=30°,∴OG=2OD=2×6=12,∴DG=![]() OD=
OD=![]() ,∴阴影部分的面积=△ODG的面积﹣扇形OBD的面积=
,∴阴影部分的面积=△ODG的面积﹣扇形OBD的面积=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】我国魏晋时期的数学家刘徽创立了“割圆术”,认为圆内接正多边形边数无限增加时,周长就越接近圆周长,由此求得了圆周率![]() 的近似值.设半径为
的近似值.设半径为![]() 的圆内接正
的圆内接正![]() 边形的周长为
边形的周长为![]() ,圆的直径为
,圆的直径为![]() .如右图所示,当
.如右图所示,当![]() 时,
时,![]() ,那么当
,那么当![]() 时,
时,![]() .(结果精确到
.(结果精确到![]() ,参考数据:
,参考数据:![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分8分)
如图,直线![]() 与双曲线
与双曲线![]() (
(![]() 为常数,
为常数,![]() )在第一象限内交于点
)在第一象限内交于点![]() ,且与
,且与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点.
两点.
(1)求直线和双曲线的解析式;
(2)点![]() 在
在![]() 轴上,且
轴上,且![]() 的面积等于
的面积等于![]() ,求
,求![]() 点的坐标.
点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线c1的顶点为A(﹣1,4),与y轴的交点为D(0,3).
(1)求c1的解析式;
(2)若直线l1:y=x+m与c1仅有唯一的交点,求m的值;
(3)若抛物线c1关于y轴对称的抛物线记作c2,平行于x轴的直线记作l2:y=n.试结合图形回答:当n为何值时,l2与c1和c2共有:①两个交点;②三个交点;③四个交点;
(4)若c2与x轴正半轴交点记作B,试在x轴上求点P,使△PAB为等腰三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下列各组数据为三角形三边,能构成直角三角形的是( )
A. 4m,8m,7m B. 2m,2m,2m C. 2m,2m,4m D. 13m,12m,5m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把RI△ABC放在直角坐标系内,其中∠CAB=90°, BC=5.点A,B的坐标分别为(1,0)、(4,0).将△ABC沿x轴向右平移,当点C落在直线 ![]() 上时,线段BC扫过的面积为( )
上时,线段BC扫过的面积为( )
A.4
B.8
C.16
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中, ∠BAC=∠ADB,BE平分∠ABC交AD于点E,交AC于点F,过点E作EG//BC交AC于点G.
(1)求证: AE=AF;
(2)若AG=4,AC=7,求FG的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com